RSDM:一種預測彈塑性結構漸近循環行為的有力直接方法

機械工程結構和結構構件經常受到循環熱-機載荷的作用，使材料的應力在非彈性範圍內超出其彈性極限。根據不同的加載水平，非彈性應變可能導致失效，由於低周疲勞或棘輪，或通過彈性安定安全。因此，估計這種結構的漸近應力狀態是很重要的。這種狀態可以通過繁瑣的增量時間步進計算來確定。相反，直接方法有很大的計算優勢，因為它們專注於這些狀態的特征，並試圖從計算開始就以直接的方式建立它們。在為數不多的通用直接方法中，文獻中出現了一種被稱為RSDM的功能強大的直接方法。該方法可以在已知載荷的精確時程的情況下直接預測任何漸近狀態。該方法的優點在於它解決了漸近循環的物理問題，並利用了其預期殘餘應力分布的循環性質。在RSDM的基礎上，還發展了一種結構安定分析方法，稱為RSDM- s。盡管采用了最直接的安定方法，RSDM-S的實現並不需要優化算法。 Both RSDM and RSDM-S may be implemented in any Finite Element Code. A thorough review of both these methods, together with examples of implementation are presented herein.

對壓力容器、飛機推進發動機、機械零件等機械工程結構來說，可變熱-機械載荷是常見的故障來源。通常這些結構和結構構件是彈性設計的。然而，為了提高它們的效率，它們經常需要在過大的負載下工作，這可能會使它們遠遠超過其彈性極限。因此，了解它們的長期結構行為和安全係數對低周疲勞或棘輪，甚至安定等現象是很重要的。穩定的德魯克型總是存在這種漸近狀態[1結構材料。如果知道加載的精確時程，則可以通過演化式逐級遞增有限元(FE)計算來達到這種狀態。然而，這種方法非常耗時，而且往往在數值上不穩定。

有很大計算優勢的一個更好的選擇是使用直接方法。這些方法從計算開始就尋求漸近狀態。另一方麵，如果不知道荷載的確切時間曆史，而隻知道它們的極限，通常情況下，直接方法是唯一的選擇。

這些方法的一個典型例子是安定分析，其中尋求提供安全狀態的極限，如安定。對這種狀態的搜索通常基於下界[2或上限[3.可塑性的安定定理。大多數數值方法被描述為數學規劃(MP)問題，它尋求找到一個目標函數(通常是加載因子)的最大值或最小值，該目標函數受各種靜態或運動學約束。屈服麵的線性化導致了使用線性規劃算法的解決方案，(例如，一項開創性的工作[4])。當約束沒有線性化時，問題被表述為非線性規劃問題(例如，最近的一些工作[5])。同時由於結構離散所用的有限元數量多，約束條件多，需要解決大尺寸優化問題。這導致了特殊的數值技術，如約簡基(如參考文獻[6)或牛頓式迭代(例如，參考文獻[7])算法。隨著計算機的出現和內點方法(IPM)的發展，極限和安定大型優化問題直到今天都是通過使用這些算法或相關技術(如參考文獻)來解決的。［8，9，10，11，12，13，14])。

除了使用MP算法的公式外，其他的數值方法也出現在文獻中。線性匹配法(LMM)最初用於提供安定極限和塑性倒塌極限[15］．這是一個將線性問題與塑性問題相匹配的迭代過程。該方法通過具有空間變化模塊的線性解序列收斂到安定載荷。它已擴展到除安定外，為受熱機械載荷的結構提供棘輪邊界[16，17］．假定荷載由恒定的一次荷載加上二次波動荷載組成。因此，得到了Bree型問題的數值解，其中恒定的機械載荷與循環熱載荷[18］．將負載分成一個常數部分和一個循環部分的類似假設也被用於下限解[19］．參考文獻[20.提出了一種估計棘輪邊界的簡化方法。它是基於參考文獻中提出的虛構的屈服麵。[21］．

LMM被擴展到尋找棘輪邊界[22]用於熱負荷和機械負荷同時循環變化。最近，文獻中提出了一種利用連續直接漸近解估計棘輪邊界的算法。[23］．

除了確定各種極限之外，重要的是要有直接的方法來確定在給定的時間曆史中荷載對結構的長期影響。解決這一問題的直接方法是直接循環分析(DCA) [24]程序，該程序已在Abaqus軟件中實現[25］．該方法基於漸近循環處的位移變為循環的假設。這是一個相當複雜的增量迭代過程的組合，它對交替塑性的情況給出了良好的結果，但對接近棘輪荷載不能收斂。另一種基於塑性應變增量的直接增量迭代方法在文獻[26］．

殘餘應力分解法(RSDM) [27]是一種通用的直接方法，可用於估計彈塑性結構在受到給定循環荷載時將發展成什麼樣的漸近循環狀態。它最初的構想是[28]來估計爬行結構的循環穩態。該方法的通用性來自於物理論證，因為它利用了在漸近狀態下殘餘應力分布的預期循環性質。因此，殘餘應力在一個加載周期內以傅立葉級數分解。利用殘餘應力時間導數迭代求出這些級數的係數，在滿足平衡和相容條件下求出周期內各時間點的殘餘應力時間導數。在RSDM的基礎上，另一種稱為RSDM- s的方法被開發出來，以建立安定限度[29］．這兩種方法在兩種或三種熱機械載荷下的應用已在文獻中介紹。［30.，31，32］．參考文獻[32， RSDM-S也被擴展到多維加載域。將該方法擴展到應用位移載荷的一些初步結果可以在參考文獻中找到。[33］．

本文將對RSDM及其改進版本RSDM- s進行全麵的介紹。還將從理論和數值的角度討論最近的進展。

文中給出了新舊兩種方法的混合結果，證明了兩種方法的魯棒性和數值效率。

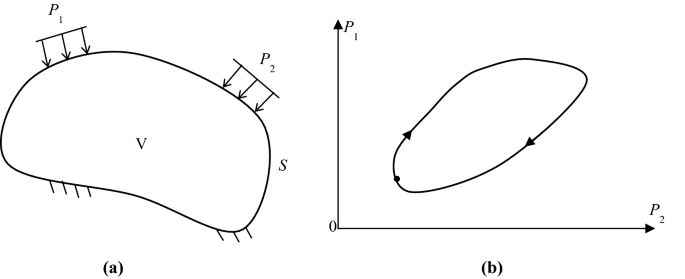
讓我們考慮一個體積為V，表麵為S的物體1)．循環加載的形式為Eq. (1)作用於S的一部分，而其餘部分在零位移條件下:

在哪裏P（t)是作用於的負載集年代；t是一個時間點，T是循環的周期，n=1,2，…，表示循環次數。這裏用粗體字表示向量和矩陣。

在圖1，例如，可以看到一組兩個加載，其在加載域中的循環性質如圖所示1(b)。

讓我們假設我們的結構是由一種完全具有彈性的塑料材料構成的。在任何時間點τ＝t/T在循環過程中，結構會形成應力場\ ({\ varvec{\σ}}(\τ)\)哪些可以分解成有彈性的部分\({\varvec{\sigma}}^{el} (\tau)\)，平衡外部載荷P（τ)，假設為完全彈性行為，且為自平衡殘餘應力部分\ ({\ varvec{\ρ}}(\τ)\)由於不彈性。因此:

應變率也有類似的分解:

殘餘應變率本身可分解為彈性部分和塑性部分[21］．因此，我們可以這樣寫:

需要注意的是殘餘應變率{\ \(\點user2 {\ varepsilon}} _ {r} ^ {{}} \)為兩個相容應變率的差{\ \({\點mathbf {\ varepsilon}}} \)(真實應變速率)和{\ \(\點user2 {e}} ^ {el} \)(假設完全彈性行為的解)本身就是一個相容應變率。

彈性應變率通過彈性矩陣與應力率相關D，而通過梯度的塑性應變速率矢量為流動規律:

在哪裏f是屈服麵。

流變學或硬性學材料的德魯克穩定性假設表明，對於兩種不同的應力狀態及其對應的塑性應變，下列不等式成立:

根據這一假設，可以證明[34在相同周期的循環加載條件下，應力和應變速率趨於穩定並趨於周期的漸近循環狀態始終存在。

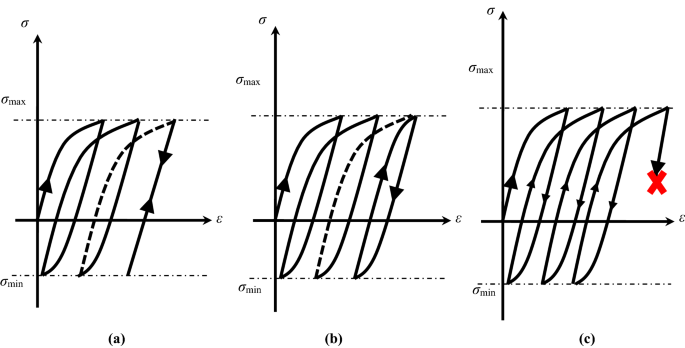
根據載荷的振幅，三種不同的漸近狀態顯示，在一維上，由圖中的應力-應變循環2，可以根據塑性應變率的存在與否來實現。

因此，對於安全狀態的彈性安定，{\ \(\點user2 {\ varepsilon}} ^ {pl} \ {\ mathbf {0}} \)．對於交替塑性(或塑性安定)的情況{\ \(\點user2 {\ varepsilon}} ^ {pl} \ ne {\ mathbf {0}}, \)但δ\ \(\點{\ user2 {\ varepsilon}} ^ {pl} = \ int_{0} ^{1}{\點{\ user2 {\ varepsilon}} ^ {pl} {d} \ \文本τ}= {\ mathbf {0}} \)結構可能因局部斷裂(低周疲勞)而失效。另一種情況是{\ \(\點user2 {\ varepsilon}} ^ {pl} \ ne {\ mathbf {0}}, \)而且\ (\ int_{0} ^{1}{\點{\ user2 {\ varepsilon}} ^ {pl} {d} \ \文本τ}\ ne {\ mathbf {0}} \)由於過度的塑性變形導致大位移，導致結構失效，導致漸進的倒塌或棘輪。

由於循環加載，彈性應力也是循環的，因此在循環的漸近應力狀態下，殘餘應力分布預期也是循環的。利用這種循環性質，可以將殘餘應力分解為傅立葉級數，並試圖找出未知的傅立葉係數。因此，我們可以寫[27]：

對上麵的式子微分τ導數可以寫成下麵的表達式:

利用三角函數的正交性質，可以得到函數的傅立葉係數的表達式餘弦而且正弦殘餘應力導數的級數:

常數項可在周期結束時利用其開始和結束時的信息估計[27]：

其中下標b和e分別表示循環的開始和結束。因此，它可以被eq所看到。（9)及(10)，通過對一個周期積分，一旦提供了殘餘應力導數，就可以估計出傅立葉係數。

這些導數可以通過在循環內的某些預定時間點施加相容性和平衡來找到。為此，我們假設我們的結構是用有限元(fe)離散化的。利用有限元網格節點的位移率，我們可以寫:

從方程式。（5B)和(4)我們可以這樣寫:

由於應變率是運動學容許的，殘餘應力率是自平衡的，並且假設，對於一個虛擬應變場，固定的支撐\(\delta \dot{\user2{\varepsilon}}_{r}\)，利用虛功原理(PVW):

結合Eq. (11)和它的虛擬形式，以及方程式。（12)及(13)，我們得到:

或者說:

在哪裏K為剛度矩陣，{\ \(\點user2 {R}} \)是由塑性應變引起的節點力的速率向量。

必須注意的是，這個公式使用兼容殘餘應變向量[33，而不是參考文獻中使用的總應變矢量。[27]，雖然，顯然導致相同的結果，需要較少的計算，因為它避免了額外的評估彈性應力的導數。

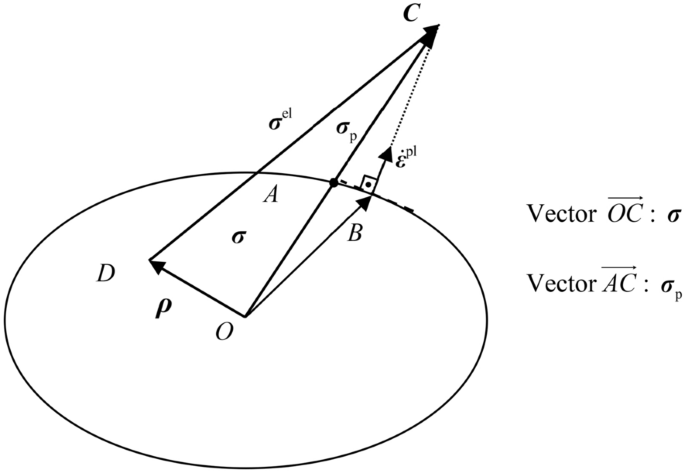
方程式中的術語。14)表示每當總應力(Eq. ()2))超過屈服麵(圖3.)．根據最近點投影[35]，返回屈服麵將，沿矢量\ (\ overrightarrow {CB} \)，為塑性應變速率{\ \({\點mathbf {\ varepsilon}}} ^ {pl} \)直接在公元前\ (\ overrightarrow {} \)．向量\ (\ overrightarrow {CA} \)等於-σ_p，這是一種沿已知向量的“徑向返回”類型的映射。這個向量，當不等於零時，稱為塑料應力向量，給出了塑料應變的等效度量。

數值計算過程

在尋找循環解的過程中，編寫了一個迭代過程，該過程在迭代中更新傅立葉係數[27］．

首先，在假定彈性的情況下求解外部荷載，得到每個循環點τ，彈性應力\({\varvec{\sigma}}^{el} (\tau)\)在連續體有限元的每一個高斯點(GP)。

讓我們假設，在迭代完成之後(μ)，是傅裏葉係數的估計\ ({\ varvec{一}}_{0}^{(\μ)},{\ varvec{一}}_ {k} ^{(\μ)},{\ varvec {b}} _ {k} ^{(\μ)}\)的存在。現在執行以下步驟:

1. 1.

   對於一個特定的循環點τ計算\({\varvec{\rho}}^{(\mu)} (\tau)\)，在每個GP，使用Eq. (7):

   $ $ {\ varvec{\ρ}}^{(\μ)}(\τ)= \壓裂{1}{2}{\ varvec{一}}_{0}^{(\μ)}+ \總和\ limits_ {k = 1} ^ {\ infty}{\左\ {{\ cos (2 k \π\τ)\ cdot {\ varvec{一}}_ {k} ^{(\μ)}+ \罪(2 k \π\τ)\ cdot {\ varvec {b}} _ {k} ^{(\μ)}}\右\}}。$ $

   （16）
2. 2.

   評估每個GP的總應力\({\varvec{\sigma}}^{(\mu)} (\tau)\)，用Eq. (2):

   $ $ {\ varvec{\σ }}_{{^{{}} }}^{\ 左(μ\ \右)}(\τ)= {\ varvec{\σ}}^ {el}(\τ)+ {\ varvec{\ρ }}_{{}}^{\ 左(μ\ \右)}(\τ)$ $

   (17)
3. 3.

   計算在每個GP處，\(\眉題{\σ}^{(\μ)}(\τ)> \ sigma_ {Y} \),在那裏\(\眉題{\σ}\)而且\ (\ sigma_ {Y} \)分別為有效屈服應力和單軸屈服應力。在這種情況下計算\({\varvec{\sigma}}_{p}^{(\mu)} (\tau)\)：

   （18)
4. 4.

   為整個結構集合節點力的速率矢量{\ \(\點user2 {R}}(\τ)\)，這是方程式的r.h.s.。（14), (15):

   $ $ \點{\ user2 {R}} ^{(\μ)}(\τ)= \ int \ limits_ {V} {{\ varvec {B}} ^ {T} \ \文本cdot {\ varvec{\σ}}_ {p} ^{\離開μ(\ \)}(\τ)文本\ d {} V}。$ $

   (19)
5. 5.

   求解以下方程的迭代形式(15)，並取得\(\dot{\user2{r}}^{(\mu)} (\tau)\)：

   $ $ \ user2 {K \點{r}} _ {r} ^{\離開μ(\ \)}(\τ)= \點{\ user2 {r}} ^{(\μ)}(\τ)$ $

   (20)
6. 6.

   在每個GP處評估殘餘應力導數率，使用方程式。（12)及(11):

   $ $ {\ varvec{\點{\ρ}}}^{{\離開μ(\ \)}}(\τ)= {\ varvec {DB \點{r}}} _ {r} ^{{\離開μ(\ \)}}\τ- {\ varvec{\σ}}_ {p} ^{{\離開μ(\ \)}}(\τ)$ $

   (21）
7. 7.

   對所有假設的循環點重複步驟1-6。

8. 8.

   對循環點進行數值積分，並利用等式更新傅裏葉係數。（9)及(10):

   $ $ \開始{聚集}{\ varvec{一}}_ {k} ^{{\離開({\μ+ 1}\右)}}= - \壓裂{1}{kπ\}\ int \ limits_{0} ^{1}{\左\{{\離開[{{\點{\ varvec{\ρ}}}^{左μ(\ \)\}\離開(\τ\右)}\右]\離開({{\文本{罪}}2 k \π\τ}\右)}\右\}{文本\ d{}} \τ},{}\ hfill \ \ {\ varvec {b}} _ {k} ^{{\離開({\μ+ 1}\右)}}= \四\壓裂{1}{kπ\}\ int \ limits_{0} ^{1}{\左\{{\離開[{{\點{\ varvec{\ρ}}}^{左μ(\ \)\}\離開(\τ\右)}\右]\離開({{\文本{因為}}2 k \π\τ}\右)}正確\ \}{文本\ d{}} \τ},{}\ hfill \ \ \壓裂{{{\ varvec{一}}_{0}^{{\離開({\μ+ 1}\右)}}}}{2}= - \ \ limits_總和{k = 1} ^ {\ infty} {{\ varvec{一}}_ {k} ^{{\離開({\μ+ 1}\右)}}}+ \壓裂{{{\ varvec{一}}_{0}^{\離開μ(\ \)}}}{2}+ \總和\ limits_ {k = 1} ^ {\ infty} {{\ varvec{一}}_ {k} ^{\μ}+}\ int \ limits_{0} ^{1}{左\[{{\點{\ varvec{\ρ}}}^{左μ(\ \)\}\離開(\τ\右)}\右]{文本\ d{}} \τ}。\hfill \\ \end{gathered}$$

   (22)
9. 9.

   從更新的傅立葉係數，評估更新的殘餘應力分布，在所有高斯點，使用Eq. (7)，並在周期結束時通過其歐氏範數檢查收斂性:

   左$ $ \壓裂{{\ \ | {{{\ varvec {\ uprho }}}_{{}}^{{\ 左({\μ+ 1}\右)}}(1)}\ \ | _{2}- \左右\ | {{{\ varvec {\ uprho }}}_{{}}^{\ 左(μ\ \右)}(1)}\右\ | _{2}}}{{\左\ | {{{\ varvec {\ uprho }}}_{{}}^{{\ 左({\μ+ 1}\右)}}(1)}\右\ | _{2}}}\勒托爾{,}$ $

   (23）

在哪裏托爾是指定的公差。

如果Eq. (23)保持時，該過程停止為循環應力狀態(cs)已收到，且\ ({{\ varvec {\ uprho}}} ^{\離開μ(\ \)}= {{\ varvec {\ uprho}}} ^{{\離開({\μ+ 1}\右)}}= {{\ varvec {\ uprho}}} ^ {cs} \)；否則，請回到步驟1並重複此過程。

一旦達到循環應力狀態，我們看\ ({{\ varvec {\ upsigma}}} _ {p} ^ {cs} = {{\ varvec {\ upsigma}}} _ {p} ^{{(\μ )}} = {{\ varvec {\ upsigma}}} _ {p} ^{{(\μ+ 1)}}\)，在最後一次迭代中進行了評估。對於每個GP，我們可以通過在周期上計算以下積分來確定得到的解的性質:

與我的所有組成部分\({{\varvec{\upsigma}} _{p}^{cs} (\tau)\)．

取決於的值\ (\ alpha_{我}\)我們可以:

1. 一)

   如果\(\alpha_{i} \ne 0\)，該GP處存在棘輪狀態。如果\(\alpha_{i} = 0\)的價值。\(\sigma_{p,i}^{cs} (\tau)\)是否檢查每個循環點τ。

2. b)

   如果\(\sigma_{p,i}^{cs} (\tau) \ne 0\)，高斯點處於反向塑性狀態，因為對於值相等但符號交替的循環點對，這必須成立。

3. c)

   如果\(\sigma_{p,i}^{cs} (\tau) = 0\)，點保持彈性或發展為彈性安定狀態。

對於所有高斯點都是彈性的或處於彈性安定狀態的情況，則結構在給定的外部荷載作用下也會安定。另一方麵，如果足夠多的GPs處於棘輪狀態，在循環狀態下，結構將發生遞增倒塌。這在數值上很容易表現出來，通過剛度矩陣的奇異性，可以在收斂的穩定循環結束時計算，通過將彈性矩陣歸零D看棘輪GPs。

例子

該程序已在開源代碼FEAP中編寫[36，使用Fortran語言。的值托爾=10⁻³證明足夠準確。展示了兩個指示性的應用例子，一個是孔板，這是一個基準的例子，和一個更複雜的例子，在幾何和邊界條件方麵，框架結構。磚單元已用於其有限元實現。用到了傅裏葉級數的三項。

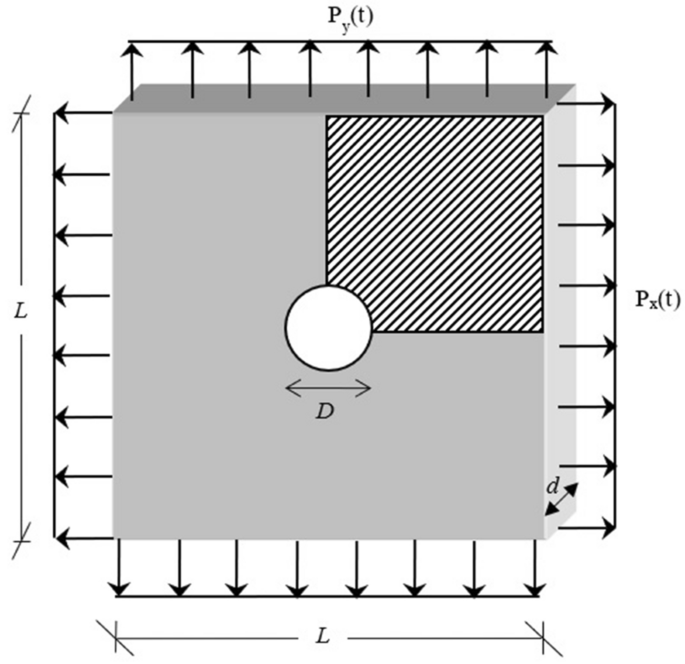
進洞板

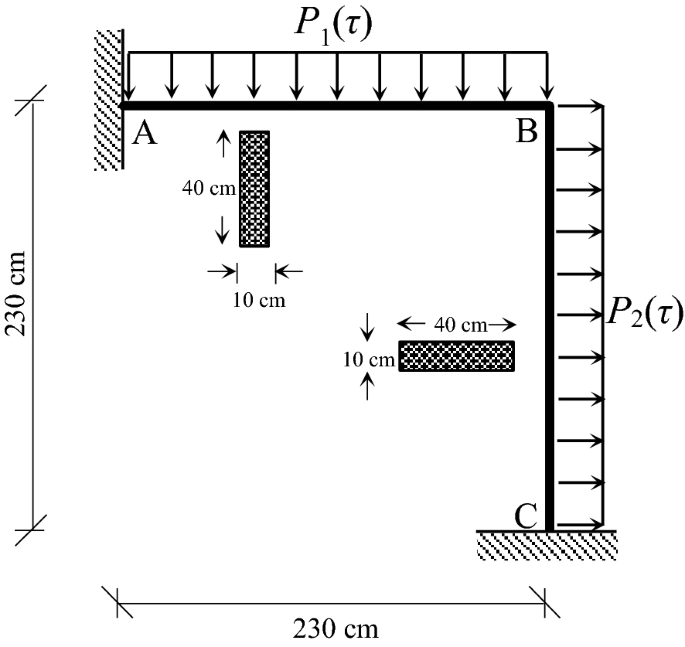
方板沿邊緣承受壓力載荷(圖4)，由於對稱性，隻有四分之一的平板是離散的，沿邊界條件X而且Y被認為是軋製的軸。讓D是圓的直徑，l平板的長度和d厚度，與\(d / l = 0.2\)，\(d/L = 0.05\)．在目前的工作中，長度l等於0.2米，材料的性能是E= 210 GPa，v= 0.3和σ_y= 360 MPa。

采用了50個時間點，隻是為了使一個周期內的應力分布看起來更平滑，盡管也可以使用更少的時間點(如30個)。

下麵實現了兩種不同的加載情況。

情況1:僅\ (P_ {x}(\τ)= 0.65 \ sigma_ {y} \罪(2 {\ uppi} \τ)\)應用。

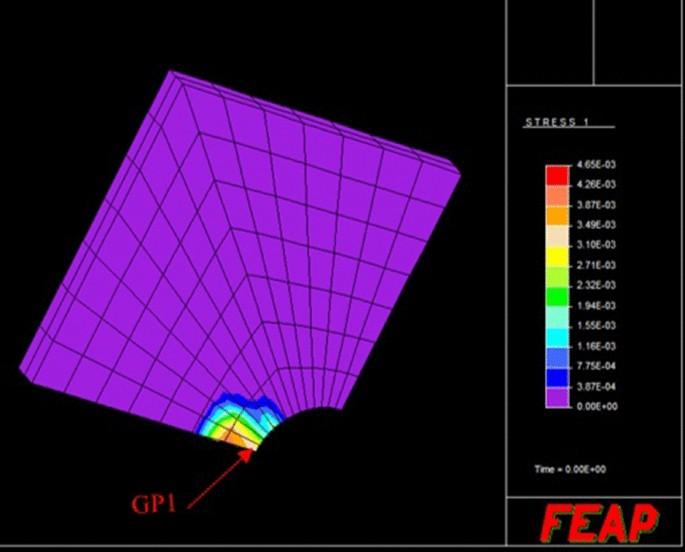
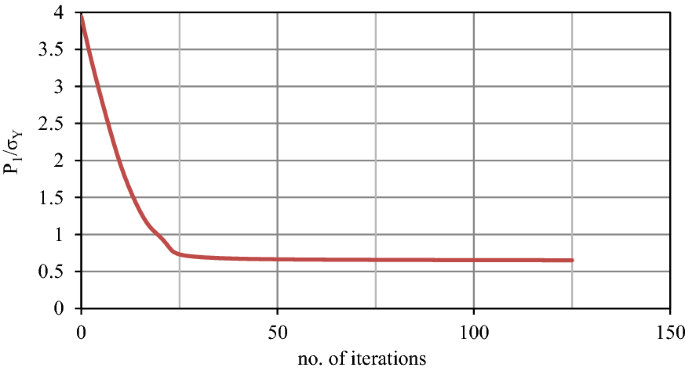
該板在196個單元中離散化(圖5)，證明結構的漸近狀態為交替塑性。人們可以看到交替的變化(圖6)，在整個循環中，最大應力高斯點GP1的塑性應力向量的一個分量。人們也可能意識到相應的積分(Eq.)24)近似為零。

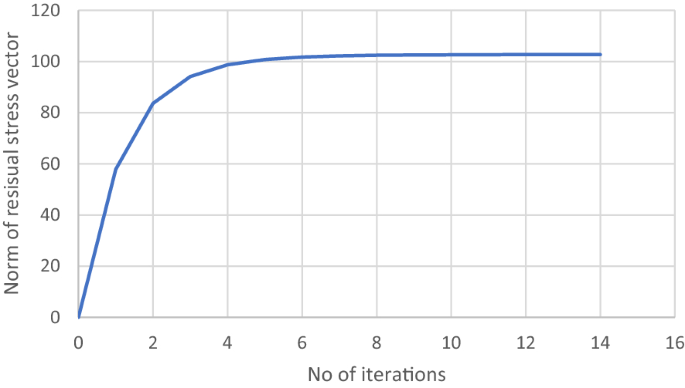
通過繪製非常小的，但在數值上非零的積分值等高線(圖5)在GP1附近具有相同行為的GPs上，局部失效機製如圖所示。最後，可以在圖中看到RSDM的收斂7．這些結果已經使用平麵元素([27)對抗時間步進程序Abaqus [25］．

情況2:施加兩個力\(P_{x} (\tau) = 0.85\sigma_{y}\)而且\(P_{y} (\tau) = 0.65\sin^{2} (2{\uppi}\tau)\)

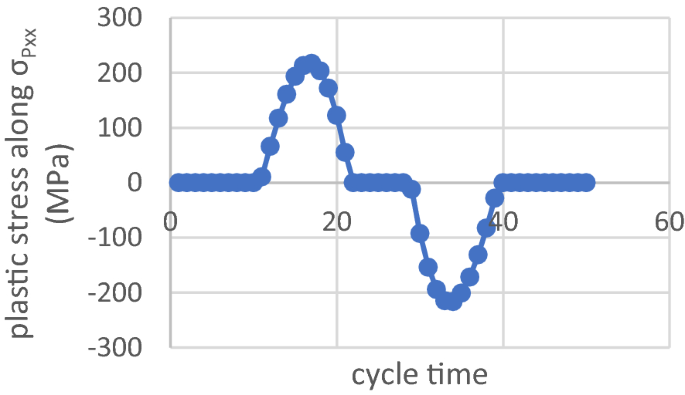
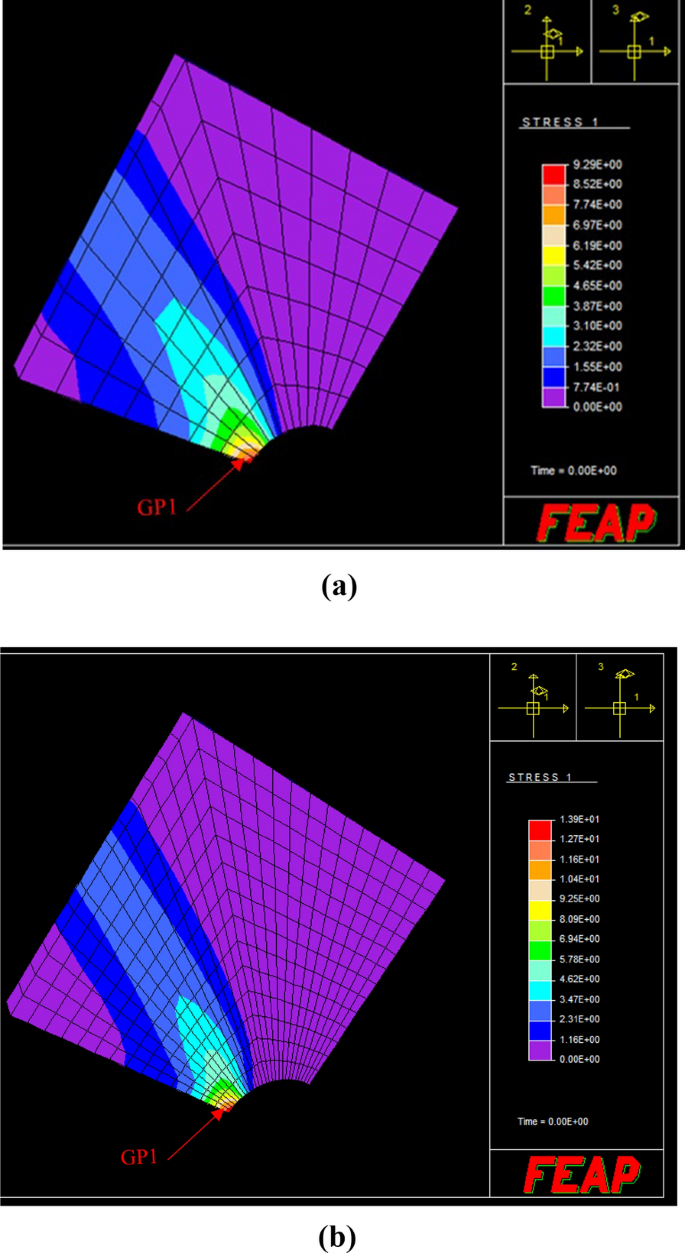
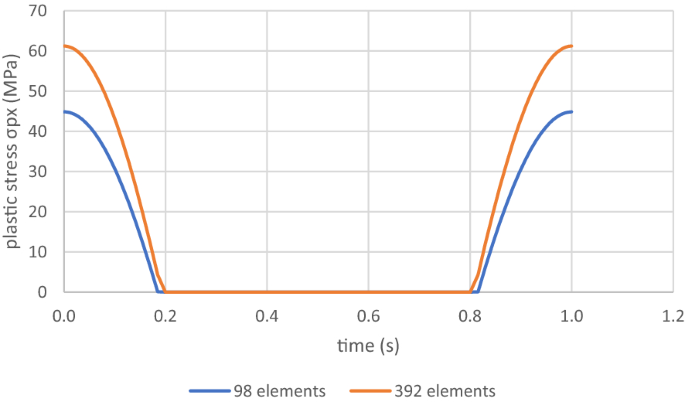
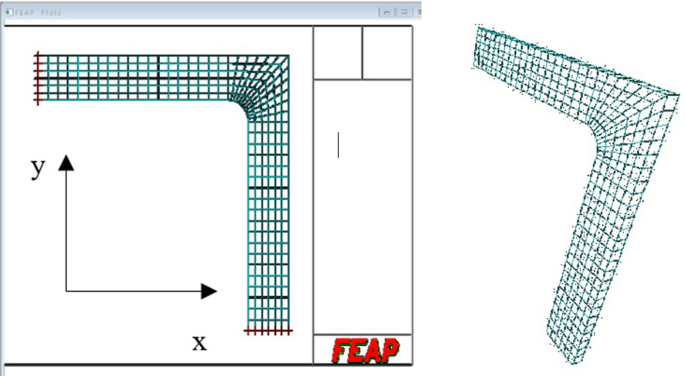
為了顯示該方法的魯棒性，我們采用了兩種不同的離散化方法，一種是粗網格，由98個元素組成(圖8(a))和一個網格更細的392個單元(圖8(b))。人們可以通過考慮RSDM預測的棘輪行為，例如，在周期內GP1處的塑性應力分布的漸近-xx分量(圖9)，顯然，在這兩種離散化的任意一種情況下，分布具有相同的符號，也呈現出積分(Eq. (24))比零大得多。

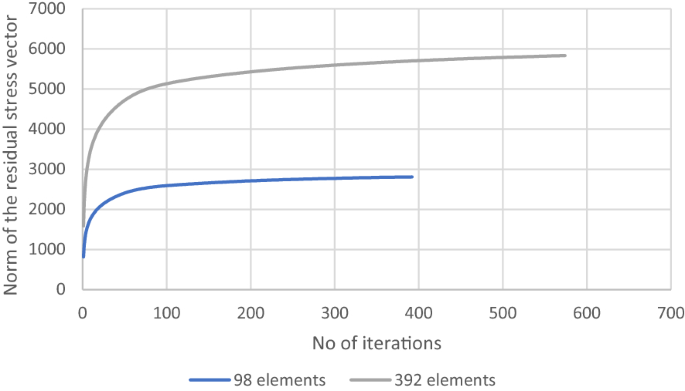
通過繪製這些積分值的等值線(圖8)，它們也具有棘輪行為，人們可能會意識到一個事實，棘輪機製出現在兩個離散化。最後，RSDM的收斂可以在圖中看到10．這些結果已在參考文獻中核查過。[27]，使用平麵元素，與時間步進程序Abaqus [25］．

框架的例子

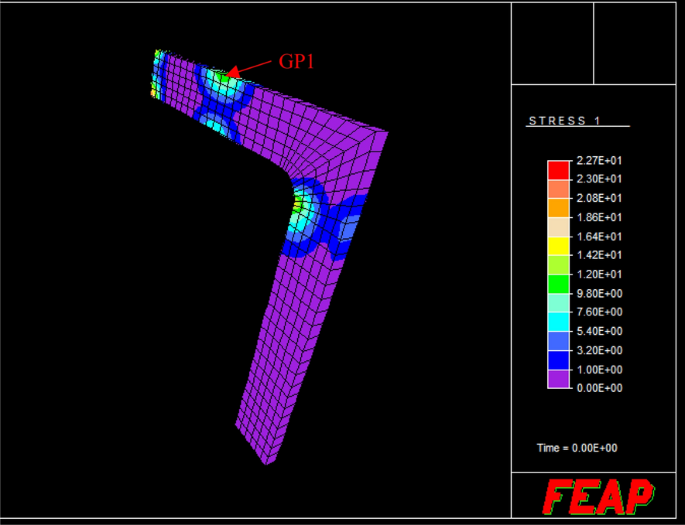
第二個應用程序示例是框架結構的示例(圖1)11)，這在參考文獻中已經考慮過。[37］．選取了以下力學性能:E= 2×10⁵N /毫米²，\ \(ν\)= 0.3,σ_y= 100 N /毫米²．結構如圖所示12由350個六邊形磚元素的8個高斯點離散。

一個加載周期內載荷的變化由:

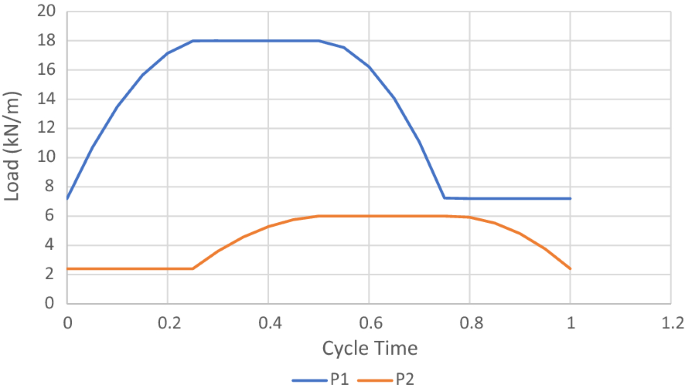
兩種負載的上述變化曲線如圖所示13．這些變化是隨機選擇的，唯一的限製是載荷最大值的比值\ (P_ {1} ^ {*} / P_ {2} ^ {*} \)等於3。這一點，在這裏可以看出一個o n圖27，在構造安定邊界的地方，產生了文獻注意到的棘輪行為[37］．事實上，RSDM預測了一個棘輪機製(圖14)，與參考文獻中所示的相當相似。[37]，它是在增量迭代算法中求得安定載荷的上界解。RSDM的優點是它的簡單性、純粹的迭代性質和解釋任何漸近行為的通用性。

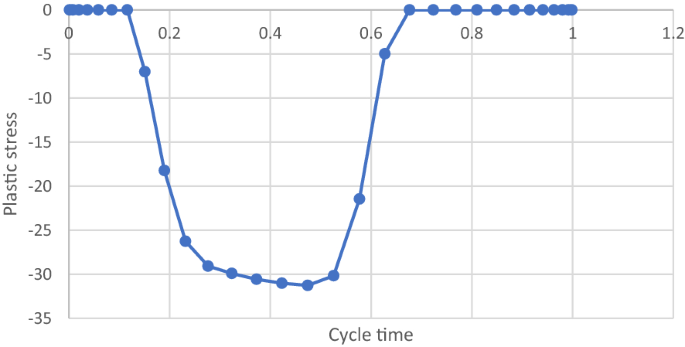
在圖15人們可以看到沿周期的變化\ (\ sigma_ {p, xx} \)塑性應力矢量在GP1處的穩態分量。所有其他穩態應力分量和棘輪機構內的所有高斯點都有這種典型的、相同符號的變化。

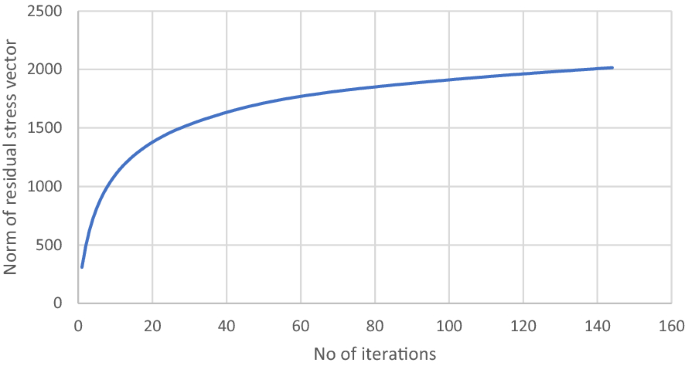
向穩態收斂的過程如圖所示16．

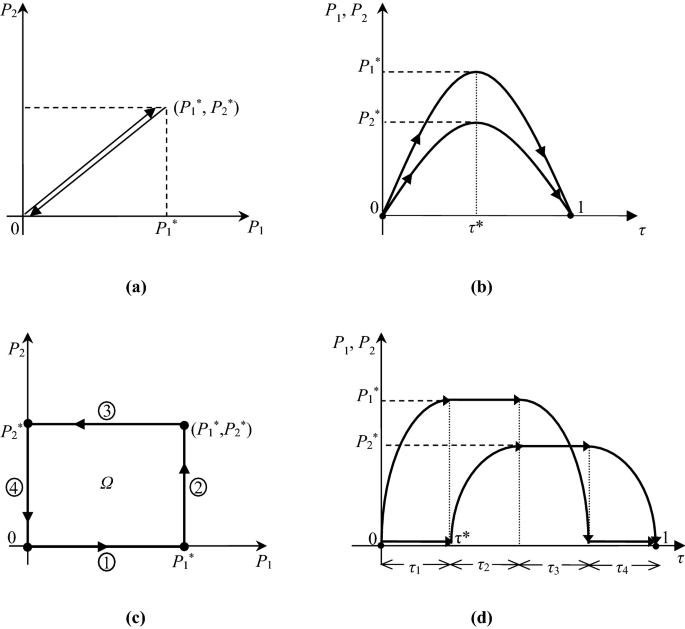
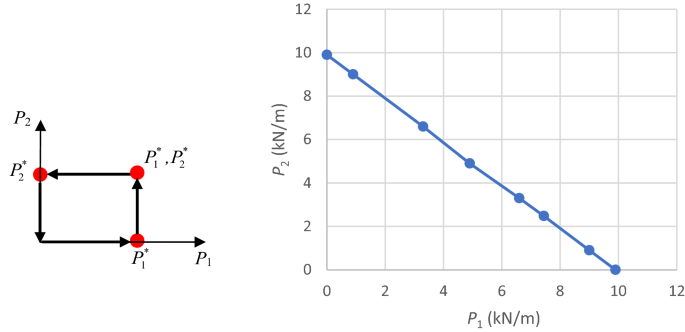
在大多數情況下，荷載的準確時間曆史是不知道的，而隻是知道它們的變化區間。安定是唯一安全的漸近狀態，提供安全裕度是很重要的。直接方法是完成這項任務的唯一途徑。負載可以按比例施加(圖17(a))或獨立(圖17(c))，介於0和的兩個極值之間\ (P_ {1} ^ {*} \)而且\ (P_ {2} ^ {*} \)對於兩種負載\ (P_ {1} ^ {{}} \)而且\ (P_ {2} ^ {{}} \),分別。光滑時間函數可以用來描述時域兩個極端之間的循環加載程序(圖17(b)及圖17(d))。當然，不同於零的兩個負載的最小值可以相應地處理。

Melan給出的彈性安定條件[2的規定如下。

1. 一)

   如果殘餘應力存在與時間無關的分布，結構在循環荷載作用下會發生搖降\(\眉題{\ user2{\ρ}}\)這樣，在規定限度內的任何載荷組合下，其與彈性應力的疊加\ ({\ varvec{\σ}}^ {el} \),也就是說,\ ({\ varvec{\σ}}^ {el} + \眉題{\ user2{\ρ}}\)，得到結構任意點處的安全應力狀態。

2. b)

   除非能找到與時間無關的殘餘應力分布，使在所有可能的載荷組合下，殘餘應力和彈性應力之和構成許用應力狀態，否則決不發生安定。

這些表述定義了受規定加載程序影響的結構的極限環。該循環的參數為安定載荷因子和時間常數殘餘應力分布，它們是唯一的，與之前的變形曆史無關[21］．

康尼錫(38]證明了如果一個結構在包含凸加載域的所有頂點的循環加載下搖動Ω，如圖所示17(c)，然後搖下任何加載路徑包含Ω．

因此，使用加載路徑頂點作為循環點的循環加載\((0 \to (P_{1}^{*}，P_{2}^{*})\ to 0)\)(適用於比例負載)或\ ((0 \ P_ {1} ^ {*} \ (P_ {1} ^ {*}, P_{2} ^{*})對P_ \ {2} ^ {*} \ 0) \)對於獨立加載，或者可以使用時域內各自循環程序的循環點。

這種循環加載，或等效的加載域，可以通過與一個因子相乘而各向同性地改變γ．通過RSDM-S程序，我們試圖找到γ_上海為此，采用循環加載使結構穩定。從上麵較高的值開始，進行一係列迭代，通過降低加載係數縮小加載域。在迭代中，RSDM用於為當前負載因子提供循環解決方案。

當滿足極限環的條件時，這個過程就停止了，殘餘應力分布中唯一剩下的傅裏葉係數是常數項。

數值計算過程

RSDM-S由兩個迭代循環組成，一個在另一個內部，外部循環由參數控製μ而內部循環由參數κ．

該程序必須從載荷係數開始，它高於安定載荷。這樣的值可以由Eq給出。(25)，得到循環點處的最小有效彈性應力非零τ^＊，例如，它可能對應於其中一個負載的最大值(參見圖17）

有了這個選擇，開始值保證大大高於安定載荷甚至極限載荷，因為所有的有限元素，至少在τ^＊，將會變成塑料。盡管有時這個值相當高，但隨著下一個迭代，這個值會大幅下降。

在初始化階段之後，即\ ({\ varvec{一}}_ {0}^ {(0)}= {\ varvec{一}}_ {k} ^ {(0)} = {\ varvec {b}} _ {k} ^ {(0)} = {\ varvec {0}} \ {\ varvec{\ρ}}_{0}^{(1)}(\τ)= {\ varvec {0}}, \)κ=1，μ=1，φ^(1）＝0，然後遵循以下迭代步驟:

使用不斷更新的外循環的負載因子，我們進入一個由κ。這個內部循環的步驟實際上與RSDM的步驟相同。

1. 1.

   下麵的表達式是針對循環點計算的τ對於網格的每個GP:

1. 2.

   檢查總有效應力是否存在\(\眉題{\σ}^{(\μ)}(\τ)> \ sigma_ {y} \)；如果不成立，我們設置\(\xi = 0\),否則:

   (27）

該操作是一個徑向返回類型規則，如圖所示3.．對每個GP重複步驟1和2。

1. 3.

   為整個結構裝配節點力的新速率向量\(\dot{\user2{R}}^{(\kappa)} (\tau)\)：

我們找到一個更新\(\dot{\user2{r}}^{(\kappa)} (\tau)\)使用關係

1. 4.

   的值\(\dot{\user2{\rho}}^{(\kappa)} (\tau)\)在每個全科醫生處進行評估。

對所有周期時間點重複步驟1-4。

1. 5.

   通過對整個周期進行數值時間積分，我們可以得到傅裏葉係數的更新:

1. 6.

   從這些更新中可以得到更新\ ({\ varvec{\ρ}}_ {(\ k + 1)} ^{(\μ- 1)}(\τ)\)用Eq的迭代形式(7):

   $ $ {{\ varvec {\ uprho}}} _ {{(\ k + 1)}} ^{{\μ- 1}}(\τ)= \壓裂{1}{2}{\ varvec{一}}_ {0}^ {{(\ k + 1)}} + \總和\ limits_ {k = 1} ^ {\ infty}{\ \{{{\文本的左側{cos (}} 2 k \π\τ)\ cdot {\ varvec{一}}_ {k} ^ {{(\ k + 1)}} +{\文本{罪(}}2 k \π\τ)\ cdot {\ varvec {b}} _ {k} ^ {{(\ k + 1)}}} \右\}}。$ $

   （32)

1. 7.

   殘餘應力傅立葉級數三角部分係數向量的範數之和為:

   $ $ \ varphi ^ {{(\ k + 1)}} = \ \ limits_總和{k = 1} ^ {\ infty}{\左\ | {{\ varvec{一}}_ {k} ^ {{(\ k + 1)}}} \右\ |}+ \總和\ limits_ {k = 1} ^ {\ infty}{\左\ | {{\ varvec {b}} _ {k} ^ {{(\ k + 1)}}} \右\ |}。$ $

   （33）

1. 8.

   是否達到循環解由以下不等式控製[32]：

   $ $ \左| {\ varphi ^ {{(\ k + 1)}} - \ varphi ^ {{(\ kappa)}}} \ | < tol。$ $

   (34)

1. 9.

   如果Eq. (34)不成立，我們設定κ=κ+1 .重複第1步;否則，我們退出內部循環並設置:

   $ $ \開始{聚集}{\ varvec{\ρ}}_{(1)}^{(\μ)}(\τ)= {\ varvec{\ρ}}_ {{(\ k + 1)}} ^{(\μ- 1)}(\τ)\ hfill \ \ \ varphi \離開({\ gamma_{{}} ^{\μ}}\右)= \ varphi ^ {{(\ k + 1)}}。\hfill \\ \end{gathered}$$

   (35）

1. 10.

   可計算加載係數的更新:

   $ $ \ gamma_{{}} ^{{\離開({\μ+ 1}\右)}}= \ gamma_{{}} ^{\離開μ(\ \)}- \ω\ cdot \ varphi \[左({\ gamma_{{}} ^{\離開μ(\ \)}}\右)]。$ $

   （36)

還應該指出的是ω是一個收斂參數，需要該參數才能使過程不繞過安定因子[29，32］．這可能與預先定義的公差有關\ (\ varphi ^ {(\ kappa)} \)哪個控製和停止迭代(例如，10⁻³, 10⁻⁴)．

在新的研究中[33，結果表明該因素是可以避免的。

1. 11.

   檢查以下不等式:

如果這不能保持，回到第1步，並開始一個新的迭代μ=μ+1;否則，已達到勒索狀態，並且:

的值可以得到準確的結果\(tol \simeq 10^{- 3}\)與δ要比托爾例:10⁻⁴_．

例子

本文介紹了RSDM-S應用的三個具有代表性的例子。隻需要傅裏葉級數中的三個項(常數項和三角級數的前兩項)。

進洞板

第一個例子是在機械和熱載荷作用下的孔板的基準例子。通過運行RSDM-S對不同的最大載荷比例得到安定域。

1. 一)

   圖的盤子4承受兩種機械載荷P₁而且P₂沿著x和y方向，分別按比例變化(圖17(a)、(b))。采用了98個磚單元的網格劃分。

可以在圖中看到安定域18和圖中典型的趨同趨勢19．

結果已在參考文獻中驗證。[29]使用參考文獻。[39］．

1. b)

   板受到兩種載荷的作用P₁而且P₂現在獨立變化(圖17(c), (d))。使用時間函數，如參考文獻中所述[29]，至少應考慮20個時間點。如果考慮的域是加載域，則隻使用5個時間點。

可以在圖中看到安定域20.，而圖中是典型的趨同趨勢21．

1. 3)

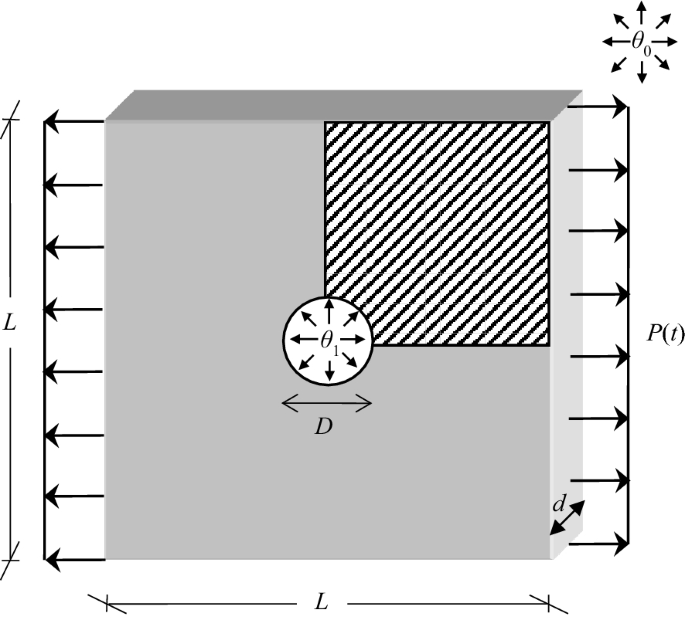
   板受到循環熱負荷和壓力負荷(圖22)．

壓力沿一側作用，溫度由內向外變化規律如下:

溫度\ (\ theta_ {0} \)取零;熱膨脹係數被認為等於\ \(5 * 10 ^{- 5} \, ^ \保監會{\文本{C}} ^ {- 1} \)．荷載以矩形荷載的形式獨立施加，在零到最大值之間，即，\(P \in [0,P^{*}]\)而且\(\Delta \theta \in [0，\Delta \theta^{*}]\)．

FE模型由200個磚塊元素組成，每個元素有8個GP(圖23)．

熱載荷引起的應力可以看作是機械載荷引起的彈性應力的附加。熱負荷和機械負荷最初在參考文獻中被考慮。[30.］．

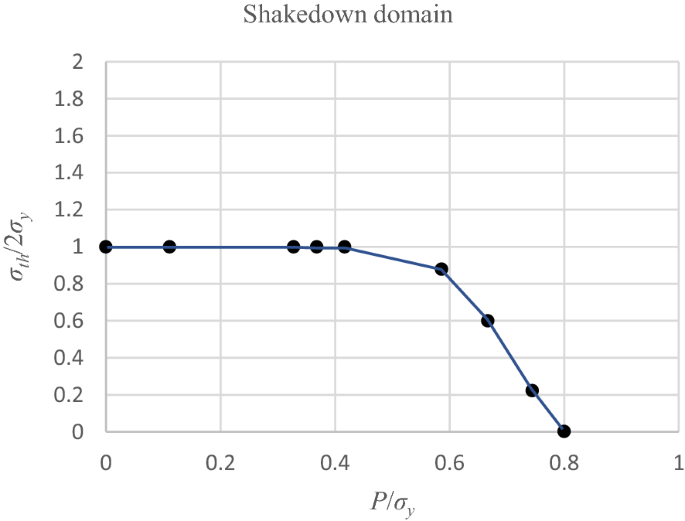
在時域內，用30個時間點的二階時間函數解決了這個問題。安定域的結果如圖所示24,在那裏\ (\ sigma_ {th} \)是由溫度波動引起的最大有效彈性熱應力。這種安定域與布裏圖非常相似[18］．參考文獻對該圖表進行了研究。[31]，其中RSDM- s和RSDM的同時使用使得一方麵可以在數值上建立安定邊界，另一方麵可以識別棘輪區域。

參考文獻[32]， RSDM-S用於產生由兩種機械載荷和熱載荷組合產生的三維安定域。證明了三維問題收斂所需要的迭代與解決二維問題所需要的迭代的順序是相同的。因此，計算時間實際上是相同的。這與使用優化算法的安定方法形成對比，因為在2D和3D情況之間，變量和約束的數量會增加一倍以上[40］．

在同一著作中([32])， RSDM-S被擴展以滿足n-維加載域，原點為零，通過自動創建循環加載程序，該程序將通過\(2^{n} - 1\)這個域的頂點。這可以通過使用組合算法(例如參考文獻[41])。

框架的例子

圖的框架結構11是下一步考慮的。研究了兩種不同的獨立加載情況。

案例1。兩個分布載荷P₁而且P₂獨立行動\(0 \le P_{1} \le P_{1}^{*}\)而且\(0 \le P_{2} \le P_{2}^{*}\)(圖17(c)， (d))，以及比值\(p_ {1}^{*} / p_ {2}^{*} = 3\)．采用400個八節點平麵應力等參有限元對框架進行離散化，高斯積分點為3×3 [29］．

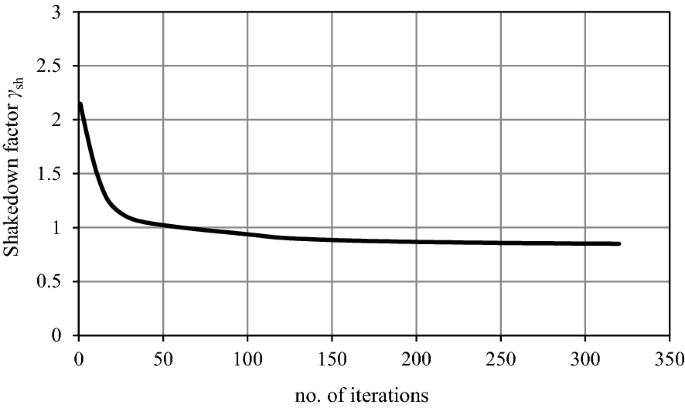
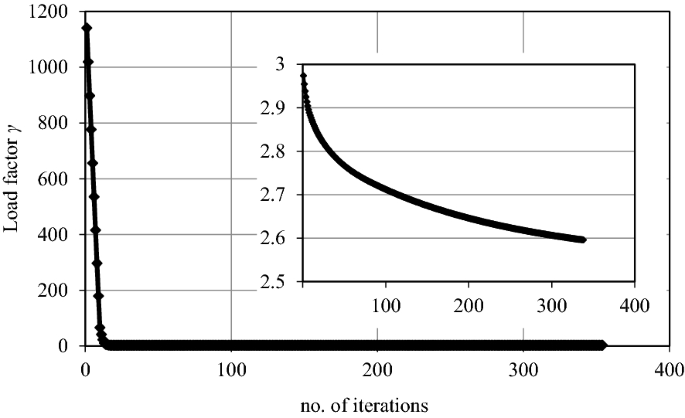
對於本例，初始收斂參數ω需要減半兩次，以便收斂，發現安定因子為2.597。可以看到，盡管過程從一個非常高的初始負載因子開始，但它下降得非常快(圖25)．在最初下降後，可以看到(插入圖)平滑收斂到安定值。

最近運行了相同的示例[33]，使用如圖所示的350個磚塊元素進行離散化12還有一個數值格式ω不需要。安定係數也大致相同，約為2.58。

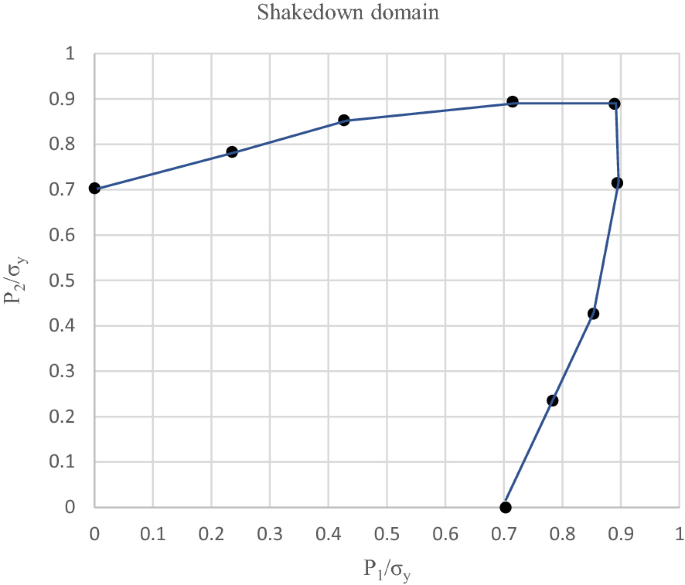
通過改變兩個荷載的極值之比，可以取類似點。因此，如圖所示的安定域26可能成立。

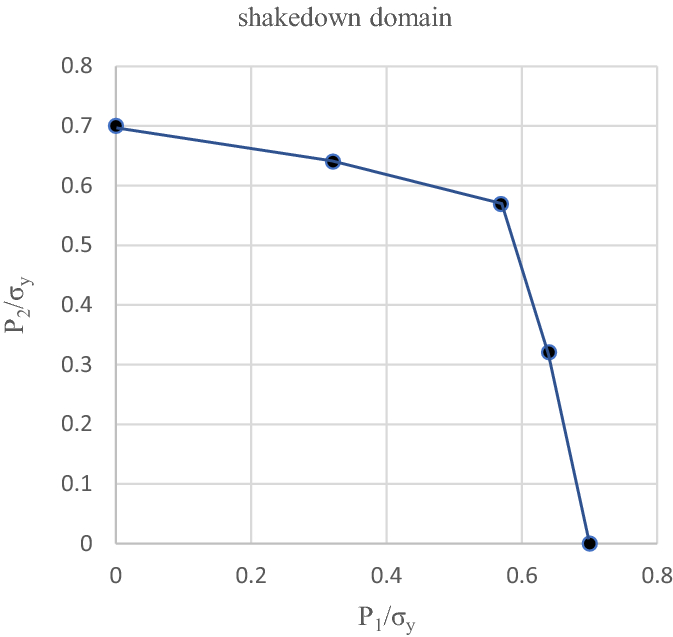
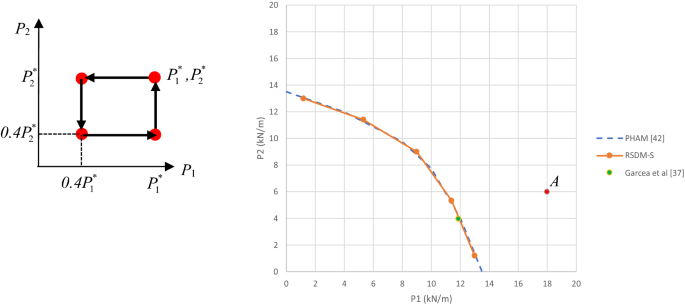
例2。接下來將嚐試負載的最小值不等於零的加載域。負載現在也獨立行動，但有以下變化:\(0.4P_{1}^{*} \le P_{1} (\tau) \le P_{1}^{*}\)而且\(0.4P_{2}^{*} \le P_{2} (\tau) \le P_{2}^{*}\)．這種類型的加載在參考文獻中已經考慮過了。[42］．RSDM-S在不同的比例下運行\ (P_ {1} ^ {*} / P_ {2} ^ {*} \)．安定域如圖所示27．有人可能會看到與Ref生成的域的完美匹配。[42]，其中使用了一種優化算法。還有，結果\(p_ {1}^{*} / p_ {2}^{*} = 3\)，在參考文獻中產生。[37]，采用應變驅動算法的增量迭代過程，使用不同的元素和密度更大的網格，實際上是在RSDM-S生成的邊界上(圖27)．

點一個，它位於穩定邊界之外，是RSDM在本工作早期用於驗證棘輪行為的方法，引用於37]和參考。[42］．

三通連接

最近，RSDM-S已加以擴展，以適應實際位移類型的負載[33］．三通廣泛應用於構成管道部件的管道元件的連接。因此，接合處可以承受劇烈的地震荷載，可以用循環施加的位移來模擬。

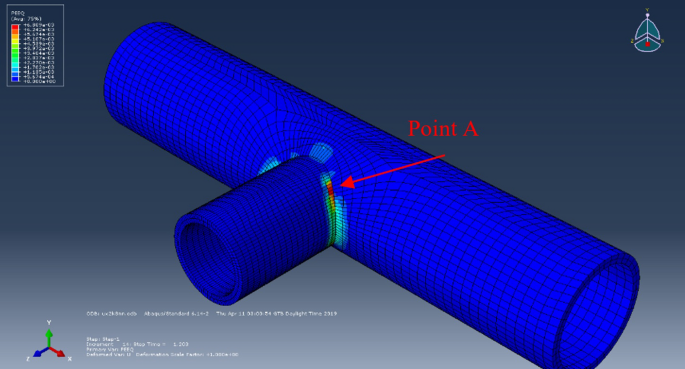
結如圖所示28由一根外徑為20.32厘米、厚度為8.18毫米的主管和一根直徑為15.24厘米、厚度為10.97毫米的稱為“支管”的副管相連。主管被認為固定在兩端，並且在分支的自由端沿分支施加位移x方向。

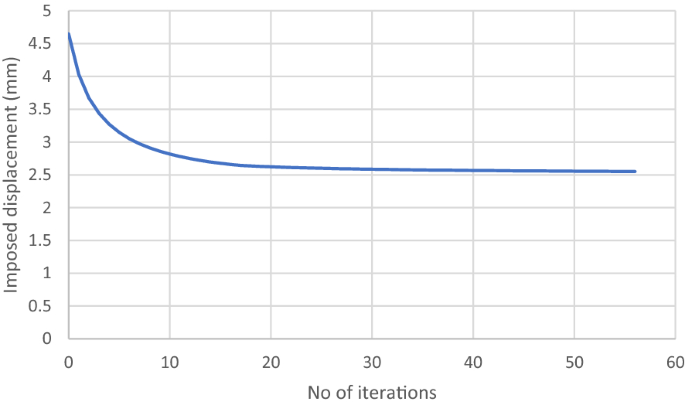
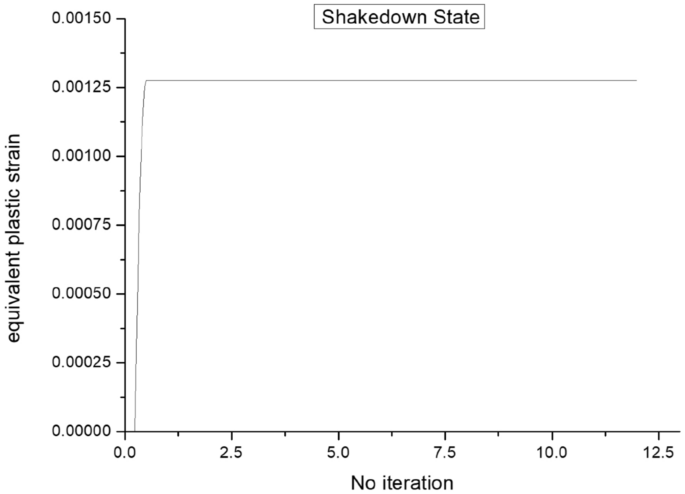
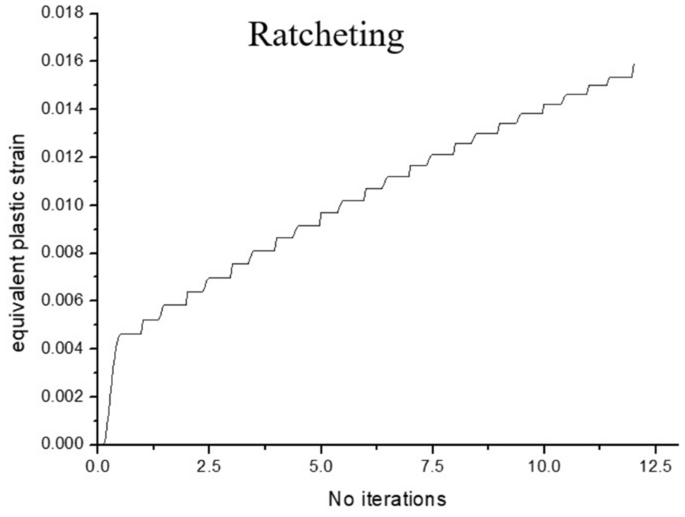
該模型由9936個磚元素組成。屈服位移等於1.43 mm。根據RSDM-S估算，沙沉位移為2.6 mm。你可以在圖中看到平滑的收斂29，根據參考文獻中討論的數值格式。[33使…ω過時了。采用Abaqus分步分析軟件對結果進行了驗證。進行了兩種不同的分析，一種在2.6 mm以下，一種在2.6 mm以上。當循環位移的最大值為2.4 mm時，人們可以看到，塑性應變的演化在第一次循環後停止(圖30.)．該圖是為壓力最大的點繪製的，也就是點一個(圖31)．你也可以在圖中看到31可塑性在這種安定狀態下的最終擴展。

另一方麵，在第二次分析中，當最大循環位移設置為3.2 mm時，塑性應變的演化是恒定的(圖1)32)在點一個，這表明已經發生了棘輪作用。

最後，從這兩種方法所研究的框架結構的共同實例來看，由於它們的共同基礎，很明顯，人們可以很容易地直接確定給定曆史的循環加載將導致結構走向什麼樣的漸近狀態，同時，當曆史未知時，這種加載的極限是什麼，將導致結構走向安全漸近狀態。

殘餘應力分解法(RSDM)是一種可以確定結構在循環荷載作用下任何一種循環漸近狀態的直接方法。該方法的威力在於，它通過利用殘餘應力的預期循環行為，直接解決了漸近循環的物理問題。在傅裏葉級數分解之後，構造了一個計算程序，以迭代的方式求出傅裏葉係數。塑性效應可以很容易地解釋，在徑向型回歸，屈服麵上，總應力矢量，這是殘餘應力和純彈性解的總和。交替塑性或漸進坍塌機製的不安全區域可以用簡單的方式表現出來。

RSDM-S是計算熱機械載荷域安定極限的一種直接方法。它解決了極限環的物理問題，其中殘餘應力在時間上是恒定的。這個過程從高的安定層開始，不斷縮小加載域，直到殘餘應力的傅裏葉分解中唯一剩下的項是常數項。

由於不需要優化算法，這兩種方法都可以在任何現有的FE代碼中實現。它們都是數值穩定和計算高效的。隻需要三個傅立葉係數，剛度矩陣隻需要分解一次。雖然馮米塞斯完美彈性塑料材料已被使用，硬化行為也可能被解釋。

不適用。

不適用。

作者和隸屬關係

1. 雅典國立技術大學土木工程係結構分析和抗震研究所，Zografou校區，希臘雅典157-80

   Konstantinos V. Spiliopoulos & Ioannis A. Kapogiannis

貢獻

KS開發了該方法的理論和數值分析部分。他還寫了手稿。IK負責編寫該方法並生成數值例子。所有作者閱讀並批準了最終稿件。

作者的信息

Konstantinos V. Spiliopoulos，生於1955年，是一名結構力學教授雅典國立技術大學(NTUA)土木工程學院結構分析與抗震研究所，希臘．他目前是這個研究所的所長。他獲得了土木工程文憑發表持有結構力學博士學位英國倫敦大學帝國理工學院航空係．他是SNAS工程專題雜誌《結構和材料的極限狀態分析與設計》的主要客座編輯。主要研究方向為計算結構力學，非彈性，材料和結構的破壞，非線性鋼筋混凝土分析。

Ioannis a . Kapogiannis, 1989年出生，目前在哈佛攻讀博士學位雅典國立技術大學(NTUA)土木工程學院結構分析與抗震研究所，希臘。他獲得了土木工程文憑帕特拉斯大學並獲得抗震結構分析與設計碩士學位發表。他的研究興趣包括結構的非彈性分析和直接方法。

相應的作者

對應到Konstantinos V. Spiliopoulos．

相互競爭的利益

作者聲明他們沒有競爭利益。

開放獲取本文遵循創作共用署名4.0國際許可協議(Creative Commons Attribution 4.0 International License)，該協議允許在任何媒體或格式中使用、分享、改編、分發和複製，隻要您給予原作者和來源適當的署名，提供創作共用許可協議的鏈接，並說明是否有更改。本文中的圖片或其他第三方材料包含在文章的創作共用許可中，除非在材料的信用額度中另有說明。如果材料不包含在文章的創作共用許可中，並且您的預期用途不被法律法規允許或超出了允許的用途，您將需要直接從版權所有者那裏獲得許可。欲查看此許可證的副本，請訪問http://creativecommons.org/licenses/by/4.0/．

轉載及權限