模糊優化設計的電動汽車防滑控製方法

至於李ORCID:orcid.org/0000 - 0002 - 8446 - 2549¹,
漢趙^1,2,
康黃^1,2&
…
Ye-Hwa陳ORCID:orcid.org/0000 - 0002 - 9591 - 1397^3,4

bwin900手机版體積34文章編號:125年(2021年)引用這篇文章

2019年訪問
指標細節

文摘

在本文中,一種新的模糊方法應用於電動汽車防滑控製的優化設計。防滑控製是用來保持車輪速度當有不確定性。控製能夠提供一個適當的扭矩輪子當車輛打滑。摩擦係數和車輪的轉動慣量和運動被認為是作為不確定的參數。這些非線性和時變有界不確定性所描述的模糊集理論。控製是確定的,而不是基於if - then模糊規則。然後,這個模糊係統的優化設計和控製成本是提出的模糊信息。通過這種方式,統一的有界性和一致最終有界性保證,平均模糊性能最小化。數值模擬表明,控製可以防止車輛打滑的最低控製成本的不確定性。

介紹

人們對環境的意識和電機和電池技術的發展,電動汽車(EVs)這些年來越來越重視1]。的防滑控製與安全是電動汽車研究領域的熱點之一。在裁判。2),快速反饋控製與電動機應用抗刹車控製。製動距離的降低了20%。在裁判。3),一個防滑控製器和PI調節器設計基於反電勢觀測器和動態模型誤差的觀察者。能得到更有效的控製方法與快速的轉矩響應和準確反饋電機的電動汽車。

然而,抗滑係統包括從電動機非線性和不確定性,輪子和道路。這些參數不能精確測量,如摩擦係數。因此,模糊方法應用於描述這個係統。

許多研究電動汽車抗側滑控製了。大多數紙使用設計參數滑移率控製。在裁判。4],sliding-mode-observer-based自適應滑模控製提出了電動汽車。在裁判。5),偏航率控製,提出了基於滑移率。在裁判。6),參數滑移率被用來為電動汽車設計滑模控製。然後,參考滑動相關道路條件需要(7,8]。這些方法是很有用的。然而,更精確的控製可能無法實現基於滑移率。在裁判。9)、道路條件提出了評估方法。這種方法是基於觀察者的驅動力,這很難適用於發動機的車輛。在裁判。10),提出了一種PI控製器沒有速度傳感器。它可以降低探測器設備速度和降低成本。但是,魯棒性不夠好基於PI控製。在裁判。11),滑模控製應用於抗滑係統的電動汽車。這種控製可以克服不確定性。

在實際的係統中是不可避免的不確定性。概率論是應用最廣泛的方法給出數學描述的不確定性和許多偉大的成就都是基於12,13]。然而,它可能並不總是適合處理不確定性通過使用發生的頻率(14]。1965年,德介紹了采用模糊集合理論來描述不確定性發生的程度(15]。最近,這個理論已經被開發和應用於許多領域,如模糊選擇(16),模糊差分方程(17]。相比之下,沒有很多探索之間的模糊集理論和係統理論。本文建立了模糊動力係統和係統的不確定性所描述的模糊集理論不同於流行的t - s模糊模型或假設的模型(18,19]。這兩個模糊模型已經應用於許多領域。在裁判。20.),模型被用來設計用於非線性動態係統的跟蹤控製。在裁判。21),考慮時間延遲問題。在裁判。22),非線性係統的保成本控製方法提出了基於Takagi-Sugeno t - s模糊模型。根據模糊動力係統基於模糊集合理論,最優設計的控製是解決模糊動力係統,當有多個可調參數。在裁判。23),建立了模糊動力係統的基本框架。在裁判。24),該理論是應用於撓性接頭操縱者。在裁判。25),一個模糊最優魯棒控製方法提出了汽車電子節氣門係統的設計。然而,隻有一個參數的優化問題被認為是以前的作品。論文的創意可以概括如下:電動汽車係統的描述不確定性的模糊集理論;設計一種新穎的高階魯棒控製;調查控製參數之間的關係,係統性能和控製成本。

主要貢獻是三倍。首先,模糊防滑建立了電動汽車動力係統。不確定性和擾動是基於模糊集理論的考慮。其次,提出了一種新的高階控製。它是確定的,而不是基於if - then模糊規則。通過應用這種控製,我們證明了係統一致有界,並通過李雅普諾夫理論一致最終有界(26]。第三,索引結合平均模糊係統性能和控製成本,提出了帶有多個參數。通過最小化索引,優化設計問題是解決了。

模糊和不確定性動力係統

在給出模糊動力係統之前,一些初步的知識與模糊集理論給出如下。

模糊數。讓\ ({\ mathfrak{年代}}\)是一個模糊集R \ (\ mathbf {} \),真正的數字。\ ({\ mathfrak{年代}}\)被稱為模糊數如果:(我)\ ({\ mathfrak{年代}}\)是正常的,(2)\ ({\ mathfrak{年代}}\)是凸的,(iii)的支持\ ({\ mathfrak{年代}}\)是有界的,(iv)\α(\ \)輕易進行關閉時間間隔R \ (\ mathbf {} \)。此外,模糊數的論域被認為是其0-cut。

模糊算法。讓\ ({\ mathfrak{年代}}\)和\ ({\ mathfrak {T}} \)兩個模糊數\ ({\ mathfrak{年代}}_{\α}= [{\ mathfrak{年代}}_{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {+}]\),\ ({\ mathfrak {T}} _{\α}= [{\ mathfrak {T}} _{\α}^ {-},{\ mathfrak {T}} _{\α}^ {+}]\)是他們的\α(\ \)輕易進行,$α\ \ [0,1]$。的加法、減法、乘法和除法\ ({\ mathfrak{年代}}\)和\ ({\ mathfrak {T}} \)定義如下,

$ $ ({\ mathfrak{年代}}+ {\ mathfrak {T}}) _{\α}= [{\ mathfrak{年代}}_{\α}^ {-}+ {\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {+}+ {\ mathfrak {T}} _{\α}^ {+}),$ $

(1)

$ $ ({\ mathfrak{年代}}- {\ mathfrak {T}}) _{\α}=[\文本{分鍾}({\ mathfrak{年代}}_{\α}^ {-}- {\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {+}- {\ mathfrak {T}} _{\α}^{+}),文本\{馬克斯}({\ mathfrak{年代}}_{\α}^ {-}- {\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {+}- {\ mathfrak {T}} _{\α}^ {+})),$ $

(2)

$ $ \開始{對齊}({\ mathfrak{年代}}\ cdot {\ mathfrak {T}}) _{\α}& =[\文本{分鍾}({\ mathfrak{年代}}_{\α}^ {-}{\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {-}{\ mathfrak {T}} _{\α}^ {+},{\ mathfrak{年代}}_{\α}^ {+}{\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {+}{\ mathfrak {T}} _{\α}^{+}),文本\ nonumber \ \ & \四\{馬克斯}({\ mathfrak{年代}}_{\α}^ {-}{\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {-}{\ mathfrak {T}} _{\α}^ {+},{\ mathfrak{年代}}_{\α}^ {+}{\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {+}{\ mathfrak {T}} _{\α}^{+})),\{對齊}$ $

(3)

$ $ \開始{對齊}({\ mathfrak{年代}}/ {\ mathfrak {T}}) _{\α}& =[\文本{分鍾}({\ mathfrak{年代}}_{\α}^ {-}/ {\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {-}/ {\ mathfrak {T}} _{\α}^ {+},{\ mathfrak{年代}}_{\α}^ {+}/ {\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {+}/ {\ mathfrak {T}} _{\α}^{+}),文本\ nonumber \ \ & \四\{馬克斯}({\ mathfrak{年代}}_{\α}^ {-}/ {\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {-}/ {\ mathfrak {T}} _{\α}^ {+},{\ mathfrak{年代}}_{\α}^ {+}/ {\ mathfrak {T}} _{\α}^ {-},{\ mathfrak{年代}}_{\α}^ {+}/ {\ mathfrak {T}} _{\α}^{+})),\{對齊}$ $

(4)

分解定理。定義一個模糊集\ (\ widehat {{\ mathfrak {D}}} _{α\}\)在\ ({\ mathfrak{你}}\)的隸屬函數\ (\ varpi _ {\ widehat {{\ mathfrak {D}}} _{\α}}= \αI_ {{\ mathfrak {D}} _{\α}}(x) \)在哪裏\ (I_ {{\ mathfrak {D}} _{\α}}(x) = 1 \)如果在{\ \ (x \ mathfrak {D}} _{α\}\)和\ (I_ {{\ mathfrak {D}} _{\α}}(x) = 0 \)如果在{\ \ (x \ mathfrak{你}},{{\ mathfrak {D}}} _{α\}\)。然後,模糊集\ ({\ mathfrak {D}} \)獲得的是

$ $ {\ mathfrak {D}} = \ bigcup \限製_ {alpha \ \ [0, 1]} \ widehat {{\ mathfrak {D}}} _{\α},$ $

(5)

在哪裏\ \ bigcup \ ()模糊集的結合(也就是說,吃晚飯在$α\ \ [0,1]$)。在此基礎上,通過他們手術後兩種模糊數\α(\ \)輕易進行,可以分解定理應用到構建生成的模糊數的隸屬函數。

D-operation。考慮一個模糊集

$ $ \ψ= \ {(\ xi, \φ(\ xi) | \ L中的ξ\ \}。$ $

(6)

對於任何函數f:R \ (L \ rightarrow \ mathbf {} \),D-operationf (\ \ (D (xi)] \)是由

$ $ D [f (\ xi)] = \壓裂{\ int _L f (\ xi)文本\φ習(\)\ D {} \ xi} {\ int _L \φ(\ xi)文本\ D {} \ xi}。$ $

(7)

\ (D (f (\ cdot)] \)代表的D-operation函數\ (f (\ cdot) \)。考慮一個模糊數習\ (\ \),一個隸屬函數\ $φ習(\ $和一個任意函數f (\ \ (xi) \)。的D-operationf (\ \ (D (xi)] \)代表的平均值f (\ \ (xi) \)在\ $φ習(\ $。本文應用D-operation給出一個確定的係統性能的表現(27]。

此外,對於任何的常數R $α\ \ \ mathbf {} $

$ $ D f (\ xi)][\αα= \ D [f (\ xi)]。$ $

(8)

證明如下:情商。7)

$ $ D[\αf (\ xi)] = \壓裂{\ int _L \αf (\ xi)文本\φ習(\)\ D {} \ xi} {\ int _L \φ(\ xi)文本\ D {} \ xi} = \α\壓裂{\ int _L f (\ xi)文本\φ習(\)\ D {} \ xi} {\ int _L \φ(\ xi)文本\ D {} \ xi} = \αD [f (\ xi)]。$ $

(9)

現在,下麵的不確定係統被認為是:

$ $ \開始{對齊}{\點{x}} (t) & = Ax (t) + (B + \δB (x (t) \σ(t), t)) (u (t) + v (t)) \ \ & \四+是(x (t) \σ(t), t), \四x (t_0) = x_0 \{對齊}$ $

(10)

在哪裏R \ (t \ \ mathbf {} \)是時間,\ (x (t) \ \ mathbf {R} ^ {n} \)是國家,\ (x_0 \)初始狀態是不確定的,\ (u (t) \ \ mathbf {R} ^ {m} \)是控製,$\σ(t) \ \ mathbf {R} ^ {p} $是一個未知時變參數,R \ (\ \ mathbf {} ^ {n \ n} \)和R \ (B \ \ mathbf {} ^ {n \乘以m} \)是已知的矩陣,v(t)是一個已知的時變向量,\ $δB (x (t) \σ(t), t)) $和\ (e (x (t) \σ(t), t)) \)分別是未知的矩陣和向量。的函數v(t),\ (e (\ cdot t) \)和\ $δB (\ cdot, t) $是連續的。的函數\ (v (\ cdot) \),\ (e (x,σ\ \ cdot) \)和\ \δB (x,σ\ \ cdot) \)勒貝格可測。

備注1

在係統(10),斧頭,B和v是線性標稱部分,δB \ (\ \)和e非線性部分。v代表可以測量的幹擾。e代表未知的不確定性和幹擾。這樣的表達式的非線性係統可以滿足匹配條件時(28]。

假設1

兩人(一個,B)的積。

假設2

對於每一個有界的入口的\ (x_0 \),即我$間的{0}$和\σ(t) (\ \),即\ $σ_i $在已知的模糊集,他們撒謊我\ (L_ {0} \)和\ (N_i \)。

$ $ L_ {0} = \ lbrace(間我{0}\φ_{\θ_i}(間的{0}))\中期間我{0}\ \θ_i \ rbrace, \;我= 1,2 \ ldots l $ $

(11)

$ $ N_{我}= \ lbrace(φ\σ_{我},\ _{我}(\σ_{我}))\中\σ_{我}\ \ω_i \ rbrace, \;i = 1 2 \ ldots, n, $ $

(12)

在哪裏$\θ_i \ \ mathbf {R} $是已知的和緊湊的論域,$\φ_{\θ_i}: \θ_i \ rightarrow [0, 1] $的隸屬函數是我\ (L_ {0} \);$\ω_i \ \ mathbf {R} $是已知的和緊湊的論域,$\φ_{\ω_i}: \ω_i \ rightarrow [0, 1] $的隸屬函數是\ (N_{我}\)。這個函數\ $σ_{我}(\ cdot) $勒貝格可測。

備注2

係統(10)模糊動力係統因為描述不確定性的模糊集合理論應用於情商。10假設2所示)。更清楚,這個模糊模型是完全不同於非常流行Takagi-Sugeno模型或其他模糊if - then規則的模型。至於處理不確定性的方法,最常見的一個是概率論。它使用發生的頻率來描述不確定性。這種解釋需要大量的數據。然而,數據的不確定性來源不能獲得或重複容易等許多實際係統的地震數據。最近,模糊集理論,作為一種替代方法,應用於描述不確定性通過發生的程度。更詳細的討論模糊集合理論的相對優勢與概率論裁判所示。29日]。

考慮下麵的黎卡提微分方程:

$ $ ^ \文本{T} P + PA-2PBR ^ {T} {1} ^ \ B文本P + Q = 0, $ $

(13)

在哪裏\ (Q > 0 \)和\ (R > 0 \)。解決方案\ (P > 0 \)如果(存在,而且是獨一無二的一個,B)是穩定化。

假設3

(我)
存在一個矩陣\ (E (x) \σ,t) \)這樣\ $δB = (x, \σ,t) $。
(2)
存在模糊數$ρ_ {E1} \ $,$ρ_ {E2} \ $,一個和b這樣,對於\ ((x, t) \ \ mathbf {R} ^ {n} \ * \ mathbf {R} \)

$ ${對齊}& \ \開始壓裂{1}{2}\λ_m (E (x, \σ,t) R ^ {1} + R ^ {1} E (x, \σ,t)) \ \ & \四\ geqslant \ρ_ {E1} >——\λ_m (R ^{1}), \{對齊}$ $

(14)

$ $ | | E (x) \σ,t) | | \ leqslant \ρ_ {E2}, $ $

(15)

$ $ | | e (x) \σ,t) | | \ leqslant | | x | | + b。$ $

(16)

備注3

不平等(14),(15)意味著不確定性不能改變的方向控製。不平等(16)意味著有一個閾值的非線性部分。我們可以獲得的極端值$ρ_ {E1} \ $因為宇宙的話語\ω_i (\ \)是已知的。基於\ $φ_i (\ cdot) $在方程式。(11),(12)、模糊算法(1)- (4)和分解定理23,30.,31日,32),相關的模糊數的隸屬度函數一個,b和$\ρ_ {E1} \ρ_ {E2} $可以計算。

通過應用控製u(t)在以下部分不確定係統(10),它可以呈現以下確定性性能:

(我)
一致有界性:對於任何\ (r > 0 \)與\ (| | x_0 | | \ leqslant r \),存在\ (d (r) > 0 \)與\ (| | x (t) | | \ leqslant d (r) \)對所有\ (t \ geqslant t_0 \)。
(2)
一致最終有界性:對於任何\ (r > 0 \)與\ (| | x_0 | | \ leqslant r \),存在${\眉題{d}} (r) > 0 $和\ (T({\眉題{d}} (r), r) \ geqslant 0 \)這樣\ (| | x (t) | | \ leqslant{\眉題{d}} (r) \)作為\ (t \ geqslant t_0 + t({\眉題{d}} (r), r) \)。

EVs抗滑係統魯棒控製設計

簡化表達式,我們\ $α= B ^ \文本{T} Px $,\ (h = \λ_m (R ^{1}) + \ρ_ {E1} \),${\眉題{一}}= a + \ρ_ {E2} | | R ^ ^ {1} B文本\ P {T} | | $,$δ= \ \壓裂{{\眉題{一}}}{\三角洲_1}+ \壓裂{b}{δ_2 \}$。然後,我們提出一種魯棒控製如下:

$ $ u (t) = - R ^ {t} {1} ^ \ B文本Px (t) - \伽馬\ psi (x (t)) R ^ {t} {1} ^ \ B文本Px (t) - v (t) $ $

(17)

在哪裏

$ $ \ psi (x) = \壓裂{(\三角洲_1 | | x | | + \δ_2)^{2 \埃塔}| | \α(x) | | ^{2 \η2}}{(\三角洲_1 | | x | | + \δ_2)^{\埃塔}| | \α(x) | | ^{\埃塔}+ \ varepsilon}。$ $

(18)

在這種控製,δ_1 > 0 \ \ (\),δ_2 \ (\ \)> 0,\ (\ \ varepsilon > 0),\伽馬> 0 (\ \)和$\ \η> 1)是標量常數。除此之外,\γ(\ $和\埃塔(\ \)最優設計參數。

備注4

控製(17)是確定的,而不是基於if - then規則。第一和第二部分用於標稱係統沒有補償的不確定性和不確定性,分別。

定理1

假設係統(10)是假設1 - 3,然後控製(17)能保證統一的有界性和一致最終有界性係統(10)。

證明

這個證明是通過李雅普諾夫極大極小方法(33,34]。考慮候選人的李雅普諾夫函數

$ $ V (x) = x ^ \文本{T} Px, $ $

(19)

在哪裏P是黎卡提微分方程的解決方案(13)。然後,求導情商。19)關於時間t

$ $ \開始{對齊}{\點{V}} (x) & = 2 x ^ \文本{T} P (Ax + B (I + E) (- R ^ {T} {1} ^ \ B文本Px - \伽馬\ psi R ^ ^ \ B{1}文本{T} Px) +是]\ \ & = x ^ {T} \文本(一個文本^ \ P {T} + PA-2PBR ^ {T} {1} ^ \ B文本P) x + 2 x ^ \文本{T} PBE (- R ^ ^ \ B{1}文本{T} Px) \ \ & \四+ 2 x ^ \文本{T} PB (I + E)(- \伽馬\ psi R ^ ^ \ B{1}文本{T} Px) + 2 x ^ \文本{T}。\{對齊}$ $

(20)

黎卡提微分方程(13)和瑞利的原則,對第一項的皇家(右手邊)的情商。20.),我們有

$ $ x ^ {T} \文本(一個文本^ \ P {T} + PA-2PBR ^ {T} {1} ^ \ B文本P) x = - x ^ \文本{T} Qx \ leqslant - \λ_m (Q) | | x | | ^ 2。$ $

(21)

的情商。15),\ $α= B ^ \文本{T} Px $,第二個任期的情商。20.),我們有

$ $ 2 x ^ \文本{T} PBE (- R ^ ^ {1} B \文本{T} Px) \ leqslant 2 | | \α| | \ρ_ {E2} | | R ^ ^ {1} B文本\ P {T} | | \, | | x | | $ $

(22)

的第三個任期RHS情商。20.),由方程式。(14),(18),\ (h = \λ_m (R ^{1}) + \ρ_ {E1} \)瑞利定律,我們可以獲得

$ $ \{對齊}開始&-2x ^ \文本{T} PB \伽馬\ psi R ^ {T} {1} ^ \ B文本Px-2x ^ \文本{T} PBE \伽馬\ psi R ^ {T} {1} ^ \ B文本Px \ \ & \四= 2(文本{T} \α^ \ R ^{1} \α)\伽馬\ psi - \α(ER ^ {1} + R ^ {1} E ^ \文本{T}) \α、γ\ psi \ \ & \四\ leqslant 2 \λ_m (R ^{1}) | | \α| | ^ 2 \伽馬\ψ2 \ρ_ {E1} | | \α| | ^ 2 \伽馬\ psi \ \ & \四= 2 \伽馬h \壓裂{(\三角洲_1 | | x | | + \δ_2)^{2 \埃塔}| | \α| | ^{2 \埃塔}}{(\三角洲_1 | | x | | + \δ_2)^{\埃塔}| | \α| | ^{\埃塔}+ \ varepsilon} \ \ & \四\ leqslant 2 \伽馬h \壓裂{(\三角洲_1 | | x | | + \δ_2)^{2 \埃塔}| | \α| | ^{2 \埃塔}- \ varepsilon ^ 2}{(\三角洲_1 | | x | | + \δ_2)^{\埃塔}| | \α| | ^{\埃塔}+ \ varepsilon} \ \ & \四= 2 \伽馬h(\三角洲_1 | | x | | + \δ_2)^{\埃塔}| | \α| | ^{\埃塔}+ 2 \伽馬h \ varepsilon。\{對齊}$ $

(23)

對於上學期的RHS情商。20.、情商。16),我們有

$ $ 2 x ^ \文本{T} PBe \ leqslant 2 | | \α| | (| | x | | + b), $ $

(24)

因此,通過結合方程式。(21)- (24),${\眉題{一}}= a + \ρ_ {E2} | | R ^ ^ {1} B文本\ P {T} | | $,我們有

$ $ \開始{對齊}{\點{V}} (x) & \ leqslant - \λ_m (Q) | | x | | ^ 2 + 2 | | \α| | \ρ_ {E2} | | R ^ ^ {1} B文本\ P {T} | | \, | | x | 2 | \ \ & \四\伽馬h(\三角洲_1 | | x | | + \δ_2)^{\埃塔}| | \α| | ^{\埃塔}+ 2 \伽馬h \ varepsilon + 2 | | \α| | (| | x | | + B) \ \ & = - \λ_m (Q) | | x | | ^ 2 + 2 \伽馬h \ varepsilon 2 \伽馬h(\三角洲_1 | | x | | + \δ_2)^{\埃塔}| | \α| | ^{\埃塔}+ 2({\眉題{一}}| | x | | + B) | | \α| |。\{對齊}$ $

(25)

接下來,我們定義的函數

$ $ G(| | \α| |)= 2 \伽馬h(\三角洲_1 | | x | | + \δ_2)^{\埃塔}| | \α| | ^{\埃塔}+ 2({\眉題{一}}| | x | | + b) | | \α| | $ $

(26)

因此,的導數\ (G(| | \α| |)\)可以獲得

文本$ $ \壓裂{\ d {} G(| | \α| |)}{文本\ d{} | | \α| |}= 2 \埃塔\伽馬h(\三角洲_1 | | x | | + \δ_2)^{\埃塔}| | \α| | ^{\η1}+ 2({\眉題{一}}| | x | | + b), $ $

(27)

自$\ \η> 1),我們可以獲得的極端點\ (G(| | \α| |)$通過讓\ $壓裂{\部分G(| | \α| |)}{\部分| | \α| |}= 0 $。

$ $ | | \α_M | | = \離開(\壓裂{2({\眉題{一}}| | x | | + b)}{2 \埃塔\伽馬h(\三角洲_1 | | x | | + \δ_2)^{\埃塔}}\右)^{\壓裂{1}{\η1}}。$ $

(28)

因為h(\ $2 \γδ_1 | | x | | + \δ_2)^{\埃塔}| | \α| | ^{\埃塔}< 0 $,如果$| | \α| | > | | \α_M | | $,然後\ $壓裂{\部分G(| | \α| |)}{\部分| | \α| |}< 0 $;如果$| | \α| | < | | \α_M | | $,然後\ $壓裂{\部分G(| | \α| |)}{\部分| | \α| |}> 0 $。因此,存在的最大價值\ (G(| | \α| |)\)。然後,我們得到

$ $ \{對齊}開始G(| | \α| |)& \ leqslant G(| | \α_M | |) \ \ & = 2 \伽馬h(\三角洲_1 | | x | | + \δ_2)^{\埃塔}| | \α_M | | ^{\埃塔}+ 2({\眉題{一}}| | x | | + b) | | \α_M | | \ \ & \ leqslant 2({\眉題{一}}| | x | | + b) | | \α_M | | \ \ & = \離開(\壓裂{2 ^{\埃塔}({\眉題{一}}| | x | | + b) ^{\埃塔}}{2 \埃塔\伽馬h(\三角洲_1 | | x | | + \δ_2)^{\埃塔}}\右)^{\壓裂{1}{\η1}}\ \ & = 2 \埃塔^{- \壓裂{1}{\η1}}\伽馬^{- \壓裂{1}{\η1}}h ^{- \壓裂{1}{\η1}}\離開(\壓裂{{\眉題{一}}| | x | | + b}{\三角洲_1 | | x | | +δ_2 \}\右)^{\壓裂{\埃塔}{\η1}}。\{對齊}$ $

(29)

的情商。29日),$δ= \ \壓裂{{\眉題{一}}}{\三角洲_1}+ \壓裂{b}{δ_2 \}$,我們有

$ $ \開始{對齊}{\點{V}} (x) & \ leqslant - \λ_m (Q) | | x | | ^ 2 + 2 \伽馬h \ varepsilon + 2 \埃塔^{- \壓裂{1}{\η1}}\伽馬^{- \壓裂{1}{\η1}}h ^{- \壓裂{1}{\η1}}\離開(\壓裂{{\眉題{一}}| | x | | + b}{\三角洲_1 | | x | | +δ_2 \}\右)^{\壓裂{\埃塔}{\η1}}\ \ & \ leqslant - \λ_m (Q) | | x | | ^ 2 + 2 \伽馬h \ varepsilon + 2 \埃塔^{- \壓裂{1}{\η1}}\伽馬^{- \壓裂{1}{\η1}}h ^{- \壓裂{1}{\η1}}\離開[馬克斯\離開(\壓裂{{\眉題{一}}}{\三角洲_1}\壓裂{b}{δ_2 \}\)\右]^{\壓裂{\埃塔}{\η1}}\ \ & \ leqslant - \λ_m (Q) | | x | | ^ 2 + 2 \伽馬h \ varepsilon + 2 \埃塔^{- \壓裂{1}{\η1}}\伽馬^{- \壓裂{1}{\η1}}h ^{- \壓裂{1}{\η1}}\離開(\壓裂{{\眉題{一}}}{\三角洲_1}+ \壓裂{b}{δ_2 \}\右)^{\壓裂{\埃塔}{\η1}}\ \ & = - \λ_m (Q) | | x | | ^ 2 + 2 \γ\埃塔\ varepsilon h + 2 \γ^{- \壓裂{1}{\η1}}\埃塔^{- \壓裂{1}{\η1}}h ^{- \壓裂{1}{\η1}}\三角洲^{\壓裂{\埃塔}{\η1}}。\{對齊}$ $

(30)

這意味著${\點{V}} $是負定所有| |x| |這樣

x $ $ | | | | > \√6{\壓裂{1}{\λ_m (Q)}(2 \γ\埃塔\ varepsilon h + 2 \γ^{- \壓裂{1}{\η1}}\埃塔^{- \壓裂{1}{\η1}}h ^{- \壓裂{1}{\η1}}\三角洲^{\壓裂{\埃塔}{\η1}})}。$ $

(31)

皇家園藝的情商。31日),\埃塔(\ \),\γ(\ \),\ \ varepsilon \ ()和\ $λ_m (Q) $都是脆的。此外,所有的宇宙的話語是緊湊,\三角洲(\ \)是有界的。因此,我們可以說${\點{V}} $是負定的足夠大| |x| |。由(28),係統一致有界和一致最終有界。

備注5

從情商。31日),參數\埃塔(\ \)和\γ(\ \)可以兩個影響的大小最終有界性。同時,控製級也由這兩個參數決定。因此,有一個控製成本之間的權衡和選擇最優的係統性能\埃塔(\ \)和\γ(\ \)當我們把方程式。(17)和(31日)作為控製成本和係統性能。

注6

一致有界性和一致最終有界性係統性能得出基於李雅普諾夫方法和一些先決條件。先決條件是至關重要的,包括小說的高階魯棒控製(17電動汽車係統(的)和假設11),(12),(14)- (16)。

最優增益設計多參數

節3,我們發現參數\埃塔(\ \)和\γ(\ \)會影響係統性能和控製成本。在本節中,將提出性能指標的最小化指數將顯示。首先,通過瑞利原理

$ $ V = x ^ \文本{T} Px \ leqslant \λ_M (P) \綠色x | | | ^ 2。$ $

(32)

因此,

x $ $ - | | | | ^ 2 \ leqslant - \壓裂{1}{\λ_M (P)} $ $

(33)

結合方程式。(30.)和(33),我們有

$ ${\點{V}} (t) \ leqslant - \壓裂{\λ_m (Q)}{\λ_m (P)} V (t) + \伽馬_ \埃塔,$ $

(34)

在哪裏$\伽馬_ \η= 2 \γ\埃塔\ varepsilon h + 2 \γ^{- \壓裂{1}{\η1}}\埃塔^{- \壓裂{1}{\η1}}h ^{- \壓裂{1}{\η1}}\三角洲^{\壓裂{\埃塔}{\η1}}$,\ (V (t_0) = x ^ \文本{T} _0Px_0 \)。這是一個微分不等式(35),和Eq的解決方案。34)可以獲得如下23]

$ $ V (t) \ leqslant \離開(V_0 \壓裂{\λ_M (P)}{\λ_M (Q)} \伽馬_ \埃塔\)\文本{exp} \離開[- \壓裂{\λ_M (Q)}{\λ_M (P)} (t-t_0) \] + \壓裂{\λ_M (P)}{\λ_M (Q)} \伽馬_ \η,$ $

(35)

對所有\ (t \ geqslant t_0 \)。因此,對於任何\ (t_s \)和任何$\τ\ geqslant t_s $

$ $ V(\τ)\ leqslant \左(V_s \ kappa \伽馬_ \埃塔\右){exp} \ \文本左[- \壓裂{1}{\ kappa}(\τ-t_s) \] + \ kappa \伽馬_ \埃塔,$ $

(36)

在哪裏\ (V_s = V (t_s) = x ^ {T} \文本(t_s) Px (t_s) \)和\ (\ kappa = \λ_M (P) / \λ_M (Q) \)。自V(\ $τ)\ geqslant \λ_m (P) | | x | | ^ 2 $由瑞利原理,情商的RHS。(36)可以被視為的上界\ $λ_m (P) | | x | | ^ 2 $。這也導致一個上界x \ (| | | | ^ 2 \)。接下來,我們

$ $ \φ_1(\伽馬_ \η,\τ,t_s) = (V_s \ kappa \伽馬_ \ eta) {exp} \ \文本左[- \壓裂{1}{\ kappa}(\τ-t_s) \],美元美元

(37)

$ $ \φ_2(\伽馬_ \η)= \ kappa \伽馬_ \埃塔。$ $

(38)

請注意,對於每個$伽馬_ \ \η,t_s $,\ $φ_1(\伽馬_ \η,\τ,t_s) \ rightarrow 0 $作為$\τ\ rightarrow \ infty $。的函數\ $φ_1 $和$φ_2 \ $被視為的瞬態和穩態部分部分係統的性能。的瞬態的整體性能\ (t_s \)可以表示為\ \ (int ^ {\ infty} _ {t_s} \φ^{2}_1(\伽馬_ \η,\τ,t_s)文本\ d{} \τ\)。

$ ${對齊}\ \開始int ^ {\ infty} _ {t_s} \φ^{2}_1(\伽馬_ \η,\τ,t_s)文本\ d{} \τ= (V_s \ kappa \伽馬_ \ eta) ^ 2 \ int ^ {\ infty} _ {t_s} {exp} \ \文本左[2 \壓裂{1}{\ kappa}(\τ-t_s) \]文本\ d{} \τ\ \ & = \離開了。(V_s \ kappa \伽馬_ \ eta) ^ 2 \離開(- \壓裂{\ kappa}{2} \) \文本{exp} \離開[\壓裂{2}{\ kappa}(\τ-t_s) \] \右| ^ {\ infty} _ {t_s} \ \ & = (V_s \ kappa \伽馬_ \ eta) ^ 2 \壓裂{\ kappa} {2}。\{對齊}$ $

(39)

我們定義的性能指標\ (J = D[αJ_p \] + D[βJ_c \] \),在那裏\ (J_p = \ int ^ {\ infty} _ {t_s} \φ^{2}_1(\伽馬_ \η,\τ,t_s)文本\ d{} \τ+ \φ^ {2}_2 \)代表了係統性能,\ (J_c = \伽馬^ 2 + \壓裂{\埃塔^ 2}{2}\)代表的是控製成本,\α(\ \)和β\ (\ \)是加權因素。自\伽馬> 0 (\ \)和$\ \η> 1),讓恒\ (\ varepsilon = \伽馬^{\壓裂{- \埃塔}{\η1}}\埃塔^{\壓裂{1}{\η1}}> 0 $。然後,$伽馬_ \ \η= 2(\伽馬^{- \壓裂{1}{\η1}}\埃塔^{- \壓裂{1}{\η1}})(h + h ^{- \壓裂{1}{\η1}}\三角洲^{\壓裂{\埃塔}{\η1}})$,D-operation (7),我們有

$ $ \{對齊}開始J(\γ,\“埃塔”,t_s) & = D[αJ_p \] + D[βJ_c \] \ \ &α= \ \離開(左D \ [(V_s \ kappa \伽馬_ \ eta) ^ 2 \壓裂{\ kappa}{2} \右)+ D[\φ^{2}_{2}(\伽馬_ \ eta)] \右)+β\ \離開伽馬^ 2 +(\ \壓裂{\埃塔^ 2}{2}\)\ \ & = \α(\ kappa _1 - \ kappa _2 \ kappa _4 \伽馬^{\壓裂{1}{\η1}}\埃塔^{\壓裂{1}{\η1}}+ \ kappa _2 \ kappa ^{\壓裂{1}{\η1}}_4 \ kappa ^{\壓裂{\埃塔}{\η1}}_5 \伽馬^{\壓裂{1}{\η1}}\埃塔^{\壓裂{1}{\η1}}+ \ kappa _3 \ kappa _6 \伽馬^{\壓裂{2}{\η1}}\埃塔^{\壓裂{2}{\η1}}\ \ & \四+ 2 \ kappa _3 \ kappa ^{\壓裂{\η2}{\η1}}_4 \ kappa ^{\壓裂{\埃塔}{\η1}}_5 \伽馬^{\壓裂{2}{\η1}}\埃塔^{\壓裂{2}{\η1}}+ \ kappa _3 \ kappa ^{\壓裂{1}{\η1}}_6 \ kappa ^{\壓裂{1}{\η1}}_7 \伽馬^{\壓裂{2}{\η1}}\埃塔^{\壓裂{2}{\η1}})+β\ \離開伽馬^ 2 +(\ \壓裂{\埃塔^ 2}{2}\右),\{對齊}$ $

(40)

在哪裏

$ ${對齊}& \ \開始kappa _1 = \壓裂{\ kappa} {2} D [V ^{2} _), \四\ kappa _2 = 2 \ kappa ^ 2 D (V_s) \四\ kappa _3 = 2 \ ^ 3 + 4 \ kappa ^ 2 \ \ & \ kappa _4 = D [h] \四\ kappa _5 = D \δ,\四\ kappa _6 = D (h ^ 2) \四\ kappa _7 = D [\△^ 2]。\ \ \{對齊}$ $

(41)

話7

考慮一個模糊數習\ (\ \),一個隸屬函數\ $φ習(\ $和一個任意函數f (\ \ (xi) \)。的D-operationf (\ \ (D (xi)] \)代表的平均值f (\ \ (xi) \)在\ $φ習(\ $(23]。

獲得解決方案的優化設計問題,偏微分算子J應用對嗎\γ(\ \)和\埃塔(\ \),分別。接下來,我們

$ $ \壓裂{\部分J}{\部分\伽馬}= 0,\壓裂{\部分J}{\部分\埃塔}= 0,$ $

(42)

在哪裏在(0,+ \γ(\ \ \ infty) \),在(1 + \埃塔(\ \ \ infty) \)。假設情商的解決方案。42)$(\伽馬_i \埃塔_i) $。解代入下麵的不平等(43),找到那些滿足:

$ $ \離開了。左\[開始\{數組}{你}{\壓裂{\部分^ J}{2}{\部分\伽馬^{2}}}和{\壓裂{\部分^ J}{2}{\部分\伽馬\部分\埃塔}}\ \{\壓裂{\部分^ J}{2}{\部分\埃塔\部分\伽馬}}和{\壓裂{\部分^ J}{2}{\部分\埃塔^{2}}}{數組}\ \端]\右| _{(\γ,\η)= \離開(\伽馬_ {J} \埃塔_ {J} \右)}> 0。$ $

(43)

表示情商的解決方案。42),也滿足情商。43),$(\伽馬^{*},\“埃塔”^ {*})$。然後,$(\伽馬^{*},\“埃塔”^ {*})$性能指標的最小值點嗎J。

EVs抗滑體係

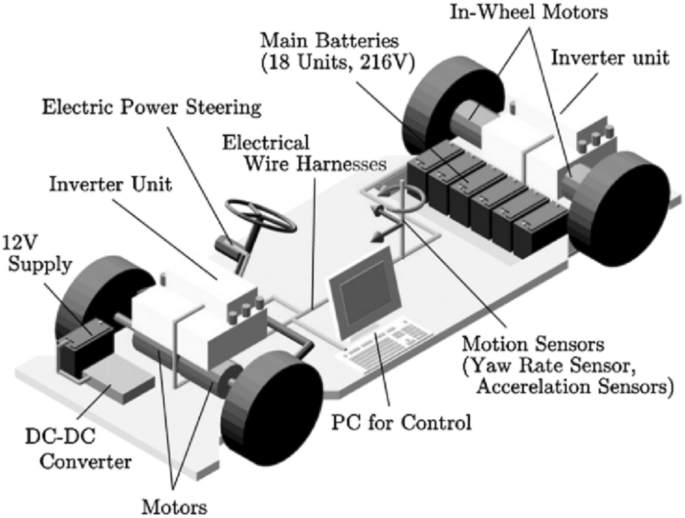
電動汽車係統如圖1(8]。傳動電機驅動車輪的前進。在本文中,重點是輪子和運動。我們的目標是控製電機提供適當的扭矩時輪之間的摩擦輪和道路是未知的。

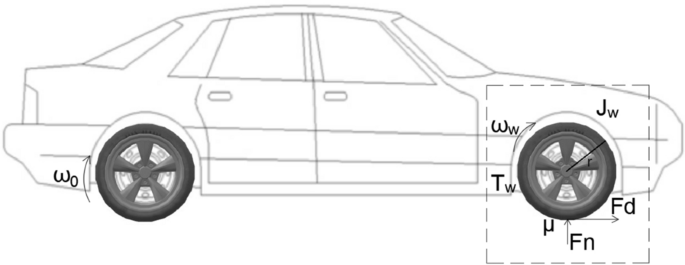
圖2顯示之間的關係電機、傳動和車輪。\ω_m (\ \),\ (T_m \)和\ (J_m \)代表著速度,電動機的輸出轉矩和轉動慣量,分別。\ω_w (\ \),\ (T_w \)和\ (J_w \)有相同的含義與車輪。傳動比是我。

從這個圖中,我們有

$ $ \ω_m (t) =我\ω_w (t) $ $

(44)

$ $ T_w (t) = iT_m (t) $ $

(45)

電動機的模型給出了如下(36]:

$ $ J_m{\點{\ω}}_m (t) = \壓裂{k_t}} {R u (t) - \壓裂{k_tk_e} {R} \ω_m (t) -B_m \ω_m (t) -T_m (t) $ $

(46)

在哪裏\ (k_t \)和\ (k_e \)的常量是電動機轉矩和電動勢,分別R是阻力,\ (B_m \)電動機的粘性阻尼係數,u是控製輸入電壓。

車輪子係統如圖3。\ω_w (\ \),\ (T_w \)和\ (J_w \)如圖2。\ (fn \)法向力的輪子,\ (F_d \)的驅動力,r輪的半徑,\ω_0 (\ \)是理想的車輪速度,\μ(\ \)是被認為是不確定性的摩擦係數。輪子的動態模型給出如下(37,38]:

$ $ J_w{\點{\ω}}_w (t) = T_w (t) -F_d r (t), $ $

(47)

$ $ F_d (t) = \μfn。$ $

(48)

結合方程式。(44)- (48),可以獲得整個係統的動態方程如下:

$ $ J_a{\點{\ω}}_w (t) = - \離開(\壓裂{k_tk_e} {R}我^ 2-B_mi ^ 2 \) \ω_w (t) - \μF_nr + \壓裂{k_ti}} {R u (t) $ $

(49)

在哪裏\ (J_a = J_mi ^ 2 + J_w \)相當於車輪和運動的時刻。

讓\ (x (t) = \ω_w (t) - \ω_0 (t) \)。因此,${\點{x}} (t) ={\點{\ω}}_w (t) -{\點{\ω}}_0 (t) $。動態方程(49)可以寫成

$ $ \開始{對齊}{\點{x}} (t) & = - \離開(\壓裂{k_tk_e} {R} + B_m \) \壓裂{i ^ 2} {J_a} x (t) \ \ & \四+左\壓裂{k_ti} {RJ_a} \ [u (t) + \壓裂{R} {k_ti} (-J_a{\點{\ω}}_0 (t) - \離開(\壓裂{k_tk_e} {R} + B_m \右)^ 2 \ω_0 (t) - \μF_nr) \右]\ \ & = {\ widehat{一}}x (t) + {\ widehat {B}} (u (t) + {\ widehat {v}} (t))。\{對齊}$ $

(50)

假設等價的時刻\ (J_a \)(39)和摩擦係數(40]\μ(\ \)是不確定性。\ (J_a ={\眉題{J}} _a + \三角洲J_a (t) \),\ $μ={\眉題{\μ}}+δ\μ(t) \ $。然後\ ({\ widehat{一}}= A + \δA \),\ ({\ widehat {B}} = B +δB \ \)和\ ({\ widehat {v}} = v +δv \ \)與

$ $ \{對齊}一開始= - \壓裂{B_a}{{\眉題{J}} _a},δ= \ \壓裂{B_a \δJ_a}{{\眉題{J}} _a({\眉題{J}} _a + \δJ_a)}, \ \ B = \壓裂{k_ti} {R{\眉題{J}} _a}, \δB = - \壓裂{k_ti \δJ_a} {R{\眉題{J}} _a({\眉題{J}} _a + \δJ_a)}, \ \ v = - \壓裂{R} {k_ti}({\眉題{J}} _a{\點{\ω}}_0 + B_a \ω_0 +{\眉題{\μ}}F_nr),δv = - \ \ \ \壓裂{R} {k_ti}(\三角洲J_a{\點{\ω}}_0 +δ\ \μF_nr), \{對齊}$ $

(51)

在哪裏\ (B_a = (k_tk_e / R + B_m) ^ 2 \)。由匹配條件,$δ= BD \ $和$δB = \ $,我們有

$ $ D = \壓裂{B_aR} {k_ti} \壓裂{\δJ_a}{{\眉題{J}} _a +δJ_a \}, E = - \壓裂{\δJ_a}{{\眉題{J}} _a +δJ_a \}, $ $

(52)

這滿足的假設3(我)。

方程式。(51)和(52),動態方程(50)可以重寫的情商。10),

$ $ e = Dx + (I + e) \δv $ $

(53)

通過選擇我\ \ (Q =),我\ \ (R =),

$ $ \壓裂{1}{2}\λ_m (ER ^ {1} + R ^ {1} E) = E . $ $

(54)

因為,\ \ (J_a > 0)和${\眉題{J}} _a > 0 $,至於E,

$ $ E = - \壓裂{\δJ_a}{{\眉題{J}} _a +δJ_a \} = \壓裂{-δJ_a \{\眉題{J}} _a +{\眉題{J}} _a}{{\眉題{J}} _a +δJ_a \} = 1 + \壓裂{{\眉題{J}} _a} {J_a} > 1, $ $

(55)

自\ $ρge 0 _ {E2} \ $,至於| |e| |,

$ $ | | e | | \ leqslant | | D | | \, | | x | | + (I + \ρ_ {E2}) | | \δv | | $ $

(56)

然後,選擇D \ (a = | | | | \),\ (b =(1 + \ρ_ {E2}) | | \δv | | \)。方程式。(54)- (56)和選擇\ $ρ_ {E1} = 0 $,\ $ρ_ {E2} = | \壓裂{\δJ_a}{{\眉題{J}} _a +δJ_a \} | $,假設3(二)滿意。

注8

適當的,不確定性\ (J_a \)和\μ(\ \)EV模型中所描述的模糊集理論。這是因為這兩個參數的物理意義不容易通過概率論解釋。此外,統一的有界性和一致最終有界性保證了不確定電動汽車係統基於模糊集理論和李雅普諾夫方法。

設計過程

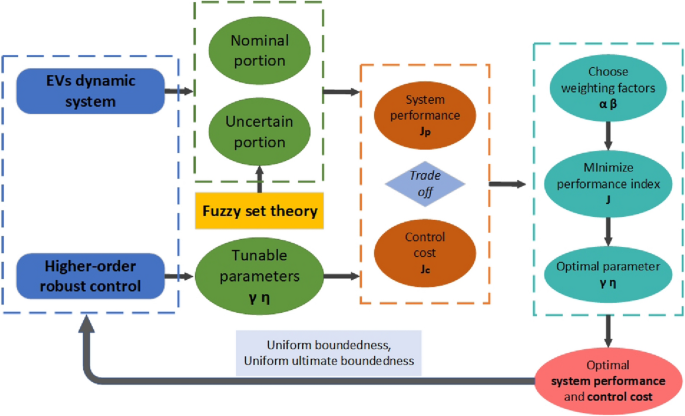
流程圖用來總結本文框架如圖4。

一方麵,建立了動力係統。此外,這個係統的不確定部分所描述的模糊集理論。另一方麵,提出了一類新穎的控製有兩個可調參數。然後,相關的成本函數對係統性能和控製成本是製定。通過最小化這個函數,我們可以獲得最優參數\γ(\ \)和\埃塔(\ \)。在此基礎上,更好的係統性能和較小的控製成本可以獲得。

仿真結果

的名義值的部分在電動汽車係統給出如下:\ (k_t = 2 \),\ (k_e = 0.4 \),\ (R = 1 \),\ (B_m = 0.1 \),\ (i = 10 \),\ \ (fn = 2000),\ (r = 0.3 \),$ω_0 = 5 \ $,{\ $\點ω_0}= 0 $,${\眉題{J}} _a = 5 $和${\眉題{\μ}}= 0.6 $。

不確定性的振幅δJ_a \ (\ \)選擇“接近0.5”,振幅的μ\三角洲(\ \ \)選擇“接近0.3”。給出相關的隸屬函數如下:

$ $ \φ_{\三角洲J_{一}}(\ν)= \左\{\開始{數組}{你}{2 \ν,}& \四{0 \ le \ν\ le 0.5}, \ \{2 \ν+ 2,}& \四{0.5 \ le \ν\勒1},{數組}\結束\ $ $

(57)

$ $ \φ_{\三角洲\μ}(\ν)= \左\{\開始{數組}{你}{\壓裂{10}{3}\ν+ 1}& \四{le \ν\ -0.3 \ le 0}, \ \{- \壓裂{10}{3}\ν+ 1。}& \四{0 \ le \ν\ le 0.3}。\結束數組{}\ $ $

(58)

然後,我們選擇的初始條件\ (x (t_s) = x (0) = 3 \)。因此,\ (V_s = 0.249 \)。基於模糊算法,\ (\ kappa _ {1 \ sim 7} \)在情商。41)可以獲得。

表1權重因素& &最優參數\ (J_{分鍾}\)

全尺寸表

通過給予不同的權重因素\α(\ \)和β\ (\ \),這意味著我們多麼關注係統性能和控製成本,不同的價值觀\γ(\ \),\埃塔(\ \)和\ (J_{分鍾}\)通過方程式。(42)和(43)。它們的值如表所示1。具體來說,參數\α(\ \)和β\ (\ \)權重因素的係統性能和控製成本,分別。在優化問題,在此優化問題,大β\ (\ \)值代表我們希望首先優化控製。在這一點上,該係統將降低控製成本為代價性能。亦然。因此,在仿真中,通過比較不同的β值和控製成本,較小的控製在預計將獲得更大的β值。最後,模擬進行使用文本$δJ_a = 0.5 | \ \{因為}(3 t) | $和文本\三角洲(\ \μ= 0.3 \{罪}(5 t) \)。選擇等方麵進行比較。選擇等方麵的原因是雙重的。首先,等方麵證明了最優控製,最小化一個性能指標,包括狀態和控製成本。第二,魯棒控製等方麵是一個證明。許多新的控製方法和等方麵相比,如模糊控製(41)和自適應控製(42]。最常見的健壯性歸因於等措施減少一半獲得任何輸入通道,無限增益放大在任何輸入通道,或相位誤差±60度在任何輸入通道。此外,有魯棒性真實模型的係數的不確定性和非線性,包括控製開關和飽和度(43]。

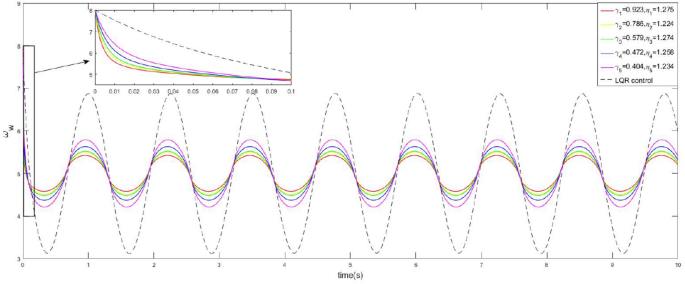
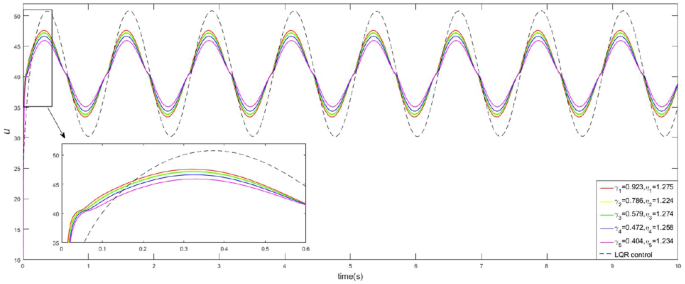
圖5顯示了車輪的速度\ω_w (\ \)曆史有不同的最優參數\γ(\ \)和\埃塔(\ \)。等方麵控製也繪製比較。它表明,提出的控製能夠渲染\ω_w (\ \)在一個較小的區域比等方麵的控製。從局部圖,我們可以發現,提出控製穩定的速度輪的速度比等方麵的控製。

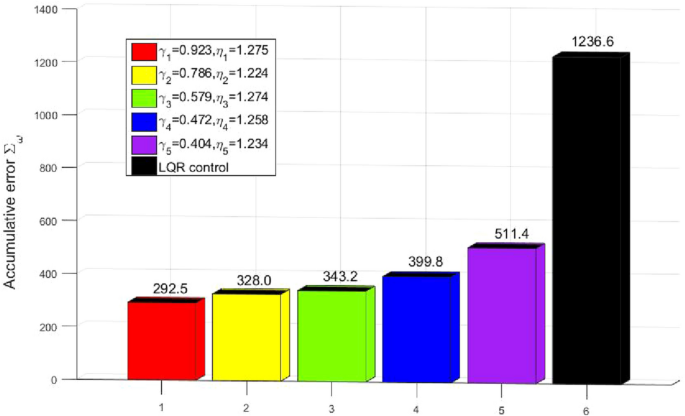
為了更清楚地顯示了係統的性能,我們定義累計誤差\ $σ_{ω\}$作為

$ $ \σ_{\ω}= \ int ^ {t_s} _{0}(\ω_w (t) - \ω_0)文本\ d {} t。$ $

(59)

圖6顯示累計錯誤\ $σ_{ω\}$在不同的控製。提出控製下的係統的累積誤差更小比累計誤差等方麵的控製之下。此外,圖5和圖6顯示係統的性能變得更好的比例加權因素\ \α/β\ \)變得更大。從一個更大的比例\ \α/β\ \)意味著我們關注更多關於係統性能比控製成本。

圖7顯示了控製輸入u曆史有不同的最優參數\γ(\ \)和\埃塔(\ \)。等方麵控製也繪製比較。可以看出,提出控製的波動小於波動等方麵的控製。

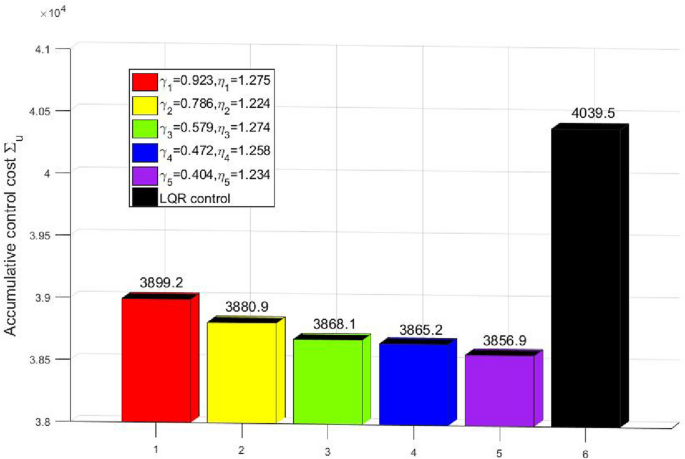
同樣的,我們定義累計控製成本\ $σ_{你}$作為

$ $ \σ_{你}= \ int ^ {t_s} _ {0} u (t)文本\ d {} t。$ $

(60)

圖8用等方麵顯示了控製成本的比較。如這個圖所示,與最優控製努力比等參數大大減少,同時展示性能優越。可以看出,累計控製成本減少的比例加權因素\ \α/β\ \)變得越來越小。從一個較小的比率意味著我們關注更多的是控製成本的係統性能。

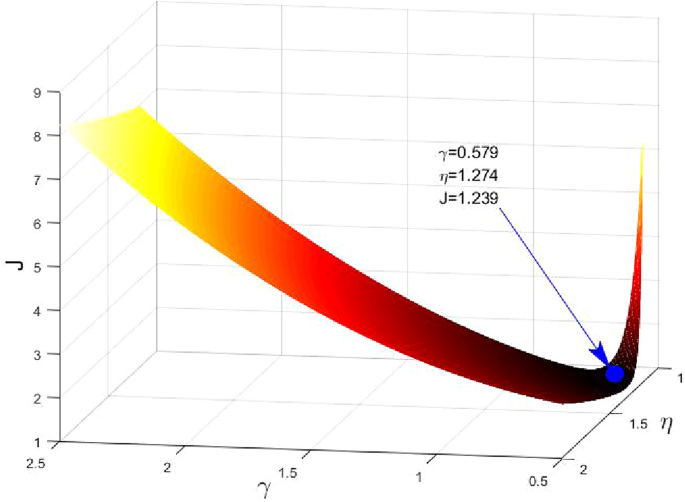
圖9顯示了性能指標之間的關係J最優參數\γ(\ \)和\埃塔(\ \)當\ $α= \β= 1 $。它的正確性驗證\ (J_{分鍾}\)這是通過方程式。(42)和(43)。

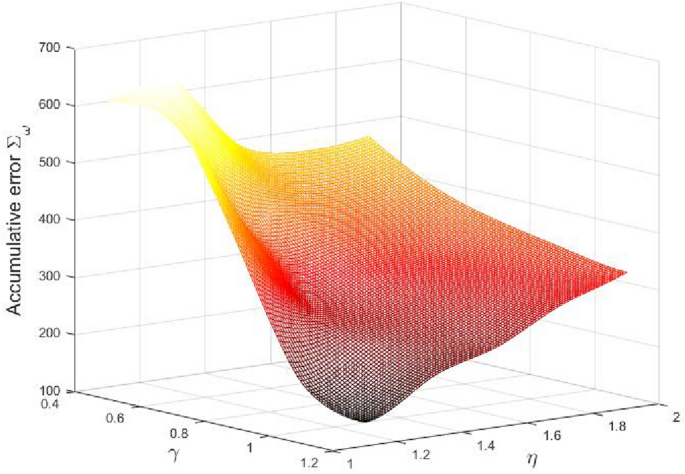
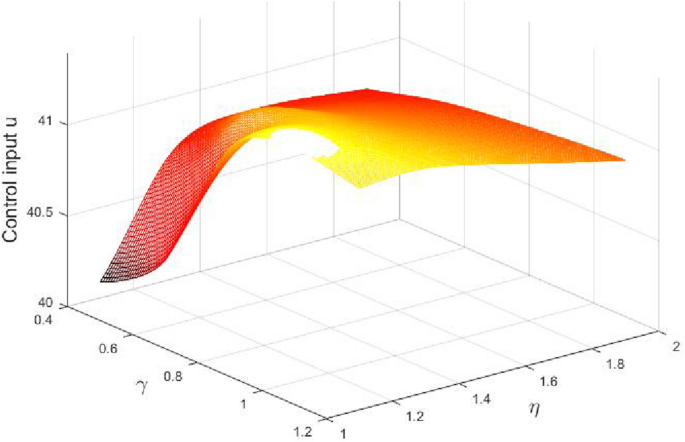
圖10和圖11顯示之間的關係\ $σ_{ω\}$,u和\γ(\ \),\埃塔(\ \),分別。它可以看到更大的\γ(\ \)呈現更好的性能和更大的控製輸入,反之亦然。然而,\埃塔(\ \)沒有這樣的單調性\ $σ_{ω\}$和u。因此,\γ(\ \)當我們關注更多的是控製成本,減少\ \α/β\ \)減少而\埃塔(\ \)總是在一個特定的值如表所示1。

結論

提出了一類高階魯棒控製的電動汽車。電動車的速度可以保持穩定時,這些控件存在不確定性。應該注意的是,基於可調參數的控製是確定的而不是if - then模糊規則。他們能夠保證統一的有界性和一致最終有界性通過李雅普諾夫極大極小係統的方法。此外,係統的不確定性和性能被模糊集合理論。然後,多參數的最優增益設計問題是考慮。一個性能指標,包括可調參數\γ(\ \)和\埃塔(\ \)提出了。通過給予不同權重因素的係統性能和控製成本,最優參數\γ(\ \)和\埃塔(\ \)可以解決通過最小化性能指標J。本文的結果表明,新提出的高階魯棒控製器可以應用於電動汽車的防滑控製。此外,本文提出的優化方法可以找到最優參數的控製器來實現更好的係統性能。

引用

C陳。過去,現在和未來電動汽車的發展。《IEEE 1999國際會議上電力電子與驅動係統,1999,1:11 - 13。
有何利的骶髂關節酒井法子,Y。利用電動機的電動汽車抗側滑控製。EPE雜誌11,2001,(4):26 - 32。
文章穀歌學術搜索
有何利的李L S玉Y。電動汽車使用的防滑控製動態模型基於反電勢觀測器誤差。IEEE 30年會的工業電子產品的社會,2004,2:1700 - 1704。
B Subudhi S S通用電氣。Sliding-mode-observer-based自適應滑動率控製電動及混合動力汽車。IEEE智能交通係統,2012,13 (4):1617 - 1626。
文章穀歌學術搜索
T Kanou H藤本。基於滑移率的偏航率控製電動汽車的傳動剛度識別。9日學報》國際研討會上先進的車輛控製,2008:786 - 791。
年代,中村K, T Kawabe et al。滑率的滑模控製電動汽車。2012年學報馬夫年會(馬夫),2012:1974 - 1979。
齋藤H藤本,T, T野口勇。運動穩定控製的電動汽車的條件下基於力矩觀察者。第八屆IEEE國際研討會上先進的運動控製2004:35 - 40。
有何利的Y。未來的車輛由電力驅動和控製研究在四個輪子駕駛汽車。第七屆國際研討會上先進的運動控製程序,2002:1 - 14。
D陰,有何利的S哦,Y。一種新的牽引力控製係統基於最大傳播轉矩估計的電動汽車。IEEE工業電子產品56,2009,(6):2086 - 2094。
文章穀歌學術搜索
H X Peng哲,G閨房,et al .防滑動調節電動汽車無速度傳感器。2009年IEEE國際研討會上工業電子產品,2009:222 - 227。
K徐,徐G, W, et al .防滑基於滑模控製的電動汽車與小說結構。2011年IEEE信息與自動化國際會議上,2011:650 - 655。
奧古斯汀,F P Coolen, G De Cooman等。介紹不精確概率。約翰威利& Sons,新澤西,2014。
書穀歌學術搜索
D Dubois, H布雷德。可能性理論及其應用:我們處在什麼位置?:施普林格手冊計算智能施普林格,紐約,2015:31-60。
R卡爾曼。隨機性進行了複查。建模、識別和控製1994年15 (3):141 - 151。
文章 MathSciNet 穀歌學術搜索
L枝。模糊集。信息和控製1965年8 (3):338 - 353。
文章 MathSciNet 穀歌學術搜索
J C R Alcantud, S·迪亞茲。合理的模糊和連續模糊選擇。模糊集和係統、2017、315:76 - 98。
文章 MathSciNet 穀歌學術搜索
Khastan, Z Alijani。新解決方案的模糊差分方程xn + 1 = a + bxn。模糊集和係統、2019、358:64 - 83。
文章 MathSciNet 穀歌學術搜索
M Sugeno G康。模糊模型的結構鑒定。模糊集與係統,1988,28 (1):15-33。
文章 MathSciNet 穀歌學術搜索
高木涉,T M Sugeno。模糊識別的係統建模和控製及其應用。IEEE係統,人,控製論,1985,(1):116 - 132。
C S曾,B S陳,H J獨角仙。通過TS模糊跟蹤控製設計非線性動態係統的模糊模型。IEEE模糊係統,2001,9 (3):381 - 392。
文章穀歌學術搜索
張Z L Chong C必應。新的t - s模糊係統的穩定性和穩定條件,隨著時間的延遲。模糊集與係統、2015、263 (C): 82 - 91。
文章 MathSciNet 穀歌學術搜索
陳X P關,C L。TS模糊係統時滯相關保證成本控製與時間延遲。IEEE模糊係統,2004,12 (2):236 - 249。
文章穀歌學術搜索
Y-H陳。一種新的模糊動力係統的控製設計方法。雜誌的動態係統、測量和控製,2011,133 (6):1 - 9。
穀歌學術搜索
J漢,陳Y-H X趙,et al。優化設計魯棒控製靈活的關節機械手:不確定的模糊動力係統的方法。國際期刊的控製、2018、91 (4):937 - 951。
文章 MathSciNet 穀歌學術搜索
趙H, H, K黃,et al。模糊最優魯棒控製方法設計的汽車電子節氣門係統。IEEE模糊係統,2017,26 (2):694 - 704。
文章穀歌學術搜索
古特曼。不確定動態著李雅普諾夫min-max方法。IEEE自動控製,1979,24 (3):437 - 443。
文章 MathSciNet 穀歌學術搜索
G J Klir B元。模糊集和模糊邏輯:理論和應用程序。普倫蒂斯霍爾PTR,新澤西,1995。
數學穀歌學術搜索
陳Y H。性能分析的不確定係統控製。動力學和控製1996 6 (2):131 - 142。
文章 MathSciNet 穀歌學術搜索
J Bezdek。特殊問題的模糊性與輸入概率n。IEEE模糊係統,1994,2 (1):1-42。
文章穀歌學術搜索
J黃,Y H陳,陳。魯棒控製的模糊動力係統:一致最終有界性和最優性。IEEE模糊係統,2012,20 (6):1022 - 1031。
文章穀歌學術搜索
H太陽,R, Y H陳,et al。優化設計的模糊魯棒控製機械係統:基於績效的泄漏和信心指數測量。IEEE模糊係統,2019,27 (7):1441 - 1455。
文章穀歌學術搜索
徐,郭Y H, H。部分模糊動力係統的魯棒控製設計:一個最優的方法。智能和模糊係統雜誌》上,2015,29 (2):553 - 569。
文章 MathSciNet 穀歌學術搜索
M J Corless。不確定非線性係統的控製。雜誌的動態係統、測量和控製、1993、115 (2 b): 362 - 372。
文章穀歌學術搜索
G作者事實上。在一個不確定係統的控製方法。學報1994年第33 IEEE會議決定和控製、1994、3:2112 - 2116。
黑爾J K。泛函微分方程。:微分方程解析理論施普林格,紐約,1971:9-22。
X嬌,沈J (T。一種自適應汽車電子油門伺服控製策略和實驗驗證。IEEE工業電子產品、2014、61 (11):6275 - 6284。
文章穀歌學術搜索
T D Gillespie。車輛動力學原理。技術報告,SAE技術論文,1992年。
Z Cai, C馬,問趙。Acceleration-to-torque比率為電動汽車防滑控製。學報2010年IEEE / ASME國際會議上機械電子和嵌入式係統和應用程序,2010:577 - 581。
W謝,D Cabecinhas, R Cunha et al。自適應反推控製四軸飛行器的不確定的車輛質量、轉動慣量和幹擾。IEEE工業電子產品,2021,1 - 1,https://doi.org/10.1109/TIE.2021.3055181。
L Walha Guerine、El哈密,et al .齒輪係統的動態響應與不確定的摩擦係數。工程軟件的進步、2018、120:45 - 54。
文章穀歌學術搜索
N S Bhangal。設計和性能等方麵和基於等雙倒立擺係統的模糊控製器。圖象圖形學報1,2013,(3):143 - 146 (2013)
文章穀歌學術搜索
理查森加法爾,T。模型參考自適應控製和quadrotor等控製參數的不確定性。國際機械和機電一體化工程雜誌》上,2015,9 (2):244 - 250。
穀歌學術搜索
B J C Doyle,弗朗西斯,R坦南鮑姆。雙重反饋控製理論。快遞公司,2013年,北切姆斯福德。
穀歌學術搜索

下載參考

確認

不適用。

資金

支持中國獎學金委員會(批準號201806690019),中國中央大學基礎研究基金(批準號300102258306),和中國安徽省自然科學基金(批準號1908085 qe194)。

作者信息

作者和聯係

合肥工業大學機械工程學院,合肥,中國
晨鳴紙業,漢趙黃&康
安徽數字設計和製造重點實驗室,合肥工業大學,合肥,中國
漢趙黃&康
公路養護設備國家工程實驗室,長安大學,西安,中國
Ye-Hwa陳
喬治·w·伍德拉夫機械工程學院的,喬治亞理工學院,美國亞特蘭大
Ye-Hwa陳

作者

至於李

看來作者出版物

你也可以搜索這個作者PubMed穀歌學術搜索
漢趙

看來作者出版物

你也可以搜索這個作者PubMed穀歌學術搜索
康黃

看來作者出版物

你也可以搜索這個作者PubMed穀歌學術搜索
Ye-Hwa陳

看來作者出版物

你也可以搜索這個作者PubMed穀歌學術搜索

貢獻

CL:軟件、寫初稿,正式的分析和模擬。YC:概念、方法、寫作和審查。KH:數據管理和監督。赫茲:資源、項目管理。所有作者閱讀和批準最終的手稿。

作者的信息

至於李(1993)目前追求的博士學位合肥工業大學機械工程學院,中國。他也是一個訪問學者喬治·w·伍德拉夫機械工程學院喬治亞理工學院,美國。他的研究興趣包括機械係統動力學優化設計的魯棒控製、自適應魯棒控製、模糊工程。

Ye-Hwa陳(1956)收到的機械工程博士學位加州大學伯克利分校,美國在1985年,。他目前是一個教授公路養護設備國家工程實驗室,長安大學,中國,還在喬治·w·伍德拉夫機械工程學院喬治亞理工學院,美國。他的研究興趣包括先進的機械係統控製方法,模糊工程、自適應魯棒控製和不確定性管理。

康黃(1968)收到了機械工程博士學位合肥工業大學,中國在2002年,。他目前是一個教授合肥工業大學機械工程學院,中國。他的研究興趣包括車輛係統動力學、機器人和汽車主動安全技術。

漢趙(1957)收到了機械工程博士學位Aalborg大學,丹麥在1990年,。他目前是一個教授合肥工業大學機械工程學院,中國。他的研究興趣包括機械係統動力學、汽車係統動力學、最優控製、自適應魯棒控製、模糊工程。

相應的作者

對應到Ye-Hwa陳。

道德聲明

相互競爭的利益

作者宣稱沒有利益衝突。

權利和權限

開放獲取本文是基於知識共享署名4.0國際許可,允許使用、共享、適應、分布和繁殖在任何媒介或格式,隻要你給予適當的信貸原始作者(年代)和來源,提供一個鏈接到創作共用許可證,並指出如果變化。本文中的圖片或其他第三方材料都包含在本文的創作共用許可證,除非另有說明在一個信用額度的材料。如果材料不包括在本文的創作共用許可證和用途是不允許按法定規定或超過允許的使用,您將需要獲得直接從版權所有者的許可。查看本許可證的副本,訪問http://creativecommons.org/licenses/by/4.0/。

再版和權限

關於這篇文章

引用這篇文章

李,C。,Zhao, H., Huang, K.et al。模糊優化設計的電動汽車防滑控製方法。下巴。j .機械工程。Eng。34125 (2021)。https://doi.org/10.1186/s10033 - 021 - 00642 - 8

下載引用

收到了:2020年4月04
修改後的:2021年4月09
接受:2021年11月03
發表:2021年12月04
DOI:https://doi.org/10.1186/s10033 - 021 - 00642 - 8

關鍵字

高階控製
模糊集合理論
不確定性
優化設計